题目内容
4.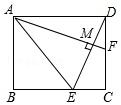 如图所示,在矩形ABCD中,F是DC上一点,AE平分∠BAF交BC于点E,且DE⊥AF,垂足为点M,BE=3,AE=2$\sqrt{6}$,则MF的长是$\frac{\sqrt{15}}{15}$.
如图所示,在矩形ABCD中,F是DC上一点,AE平分∠BAF交BC于点E,且DE⊥AF,垂足为点M,BE=3,AE=2$\sqrt{6}$,则MF的长是$\frac{\sqrt{15}}{15}$.
分析 设MD=a,MF=x,利用△ADM∽△DFM,得到a2=$\sqrt{15}$x,利用△DMF∽△DCE,则$\frac{MD}{DC}$=$\frac{MF}{EC}$,即:$\frac{MD}{MF}$=$\frac{DC}{EC}$.得到a与x的关系式,化简可得x的值,得到MF=$\frac{\sqrt{15}}{15}$.
解答 解:∵AE平分∠BAF交BC于点E,且DE⊥AF,∠B=90°,
∴AB=AM,BE=EM=3,
又∵AE=2$\sqrt{6}$,
∴AM=$\sqrt{A{E}^{2}-E{M}^{2}}$=$\sqrt{24-9}$=$\sqrt{15}$,
设MD=a,MF=x,
∵在△ADM和△DFM中,∠AMD=∠DMF,∠ADM=∠DFM
∴△ADM∽△DFM,
∴$\frac{DM}{AM}$=$\frac{FM}{DM}$,
∴DM2=AM•MF,
∴a2=$\sqrt{15}$x,
∵∠DMF=∠C,∠MDF=∠MDF,
∴△DMF∽△DCE,
∴$\frac{MD}{DC}$=$\frac{MF}{EC}$,即:$\frac{MD}{MF}$=$\frac{DC}{EC}$.
∴$\frac{a}{x}$=$\frac{\sqrt{15}}{\sqrt{(3+a)^{2}-15}}$,
∴$\left\{\begin{array}{l}{{a}^{2}=\sqrt{15}x\\}\\{\sqrt{15}x=a•\sqrt{(3+a)^{2}-15}}\end{array}\right.$,
解之得:$\left\{\begin{array}{l}{a=1}\\{x=\frac{\sqrt{15}}{15}}\end{array}\right.$,
故答案是:$\frac{\sqrt{15}}{15}$.
点评 本题考查了角平分线的性质以及三角形相似的判定方法,解题的关键在于利用三角形相似构造方程求得对应边的长度.

| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 无实数根 | D. | 两根异号 |
| A. | 2b<a+c | B. | 2b=a+c | C. | 2b>a+c | D. | a+b=c |
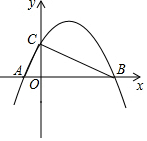 如图,在平面直角坐标系中,抛物线y=ax2+bx+4与坐标轴分别交于点A、点B、点C,并且∠ACB=90°,AB=10.
如图,在平面直角坐标系中,抛物线y=ax2+bx+4与坐标轴分别交于点A、点B、点C,并且∠ACB=90°,AB=10. △ABC中,AB=18cm,BC=6cm,BD平分∠ABC交AC于D,DE⊥AB于E,S△ABC=36cm2,则DE=3cm.
△ABC中,AB=18cm,BC=6cm,BD平分∠ABC交AC于D,DE⊥AB于E,S△ABC=36cm2,则DE=3cm. 如图,BE是△ABC的角平分线,过点E作ED⊥BC于D,若AB=4,DE=2,则△ABE的面积是6.
如图,BE是△ABC的角平分线,过点E作ED⊥BC于D,若AB=4,DE=2,则△ABE的面积是6. 如图,在平面直角坐标系中的三点A(1,0),B(-1,0),P(0,-1),将线段AB沿y轴向上平移m(m>0)个单位长度,得到线段CD,二次函数y=a(x-h)2+k的图象经过点P、C、D.
如图,在平面直角坐标系中的三点A(1,0),B(-1,0),P(0,-1),将线段AB沿y轴向上平移m(m>0)个单位长度,得到线段CD,二次函数y=a(x-h)2+k的图象经过点P、C、D.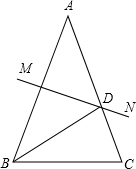 如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,则∠DBC=30度.
如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,则∠DBC=30度.