题目内容
5.已知a,b,c为正数,若二次方程ax2+bx+c=0有两个实数根,求证:方程a2x2+b2x+c2=0有两个不相等的负的实数根.分析 由二次方程ax2+bx+c=0有两个实数根,得到△1=b2-4ac≥0,于是得到(b2-4ac)(b2+4ac)=b4-4a2c2≥0,推出方程a2x2+b2x+c2=0有两个实数根,设方程a2x2+b2x+c2=0的实数根为x1,x2,求得x1+x2=-$\frac{{a}^{2}}{{b}^{2}}$<0,x1x2=$\frac{{a}^{2}}{{c}^{2}}$>0,于是得到结论.
解答 证明:∵二次方程ax2+bx+c=0有两个实数根,
∴△1=b2-4ac≥0,
∵a,b,c为正数,
∴b2+4ac>0,
∴(b2-4ac)(b2+4ac)=b4-4a2c2≥0,
∴方程a2x2+b2x+c2=0有两个实数根,
设方程a2x2+b2x+c2=0的实数根为x1,x2,
∴x1+x2=-$\frac{{a}^{2}}{{b}^{2}}$<0,x1x2=$\frac{{a}^{2}}{{c}^{2}}$>0,
∴方程a2x2+b2x+c2=0有两个不相等的负的实数根.
点评 本题考查了根的判别式,解决本题的关键是能够结合一元二次方程的根与系数的关系判断方程根的符号.

练习册系列答案
相关题目
16.方程x2-4x-5=0的二次项系数和一次项系数分别为( )
| A. | 1和4 | B. | 1和-4 | C. | 1和-5 | D. | 1和5 |
13.在实数-4、2、0、-1中,最小数与最大数的积是( )
| A. | -2 | B. | 0 | C. | 4 | D. | -8 |
20.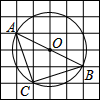 如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点,作△ABC的外接圆⊙O,则弧AC的长等于( )
如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点,作△ABC的外接圆⊙O,则弧AC的长等于( )
 如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点,作△ABC的外接圆⊙O,则弧AC的长等于( )
如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点,作△ABC的外接圆⊙O,则弧AC的长等于( )| A. | π | B. | $\frac{\sqrt{10}π}{2}$ | C. | $\frac{\sqrt{5}π}{4}$ | D. | $\frac{\sqrt{5}π}{2}$ |
10.如图是一个几何体的三视图,则这个几何体是( )


| A. | 圆锥 | B. | 圆柱 | C. | 三棱锥 | D. | 长方体 |
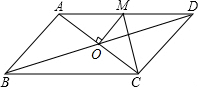 如图,?ABCD的对角线交于点O,且AD>CD,过点O作OM⊥AC,交AD于M,如果△CDM的周长为3,那么平行四边形ABCD的周长是6.
如图,?ABCD的对角线交于点O,且AD>CD,过点O作OM⊥AC,交AD于M,如果△CDM的周长为3,那么平行四边形ABCD的周长是6.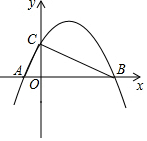 如图,在平面直角坐标系中,抛物线y=ax2+bx+4与坐标轴分别交于点A、点B、点C,并且∠ACB=90°,AB=10.
如图,在平面直角坐标系中,抛物线y=ax2+bx+4与坐标轴分别交于点A、点B、点C,并且∠ACB=90°,AB=10.