题目内容
19.阅读下列材料,并解答问题:材料:将分式$\frac{{{x^2}-x+3}}{x+1}$拆分成一个整式与一个分式(分子为整数)的和的形式.
解:由分母x+1,可设x2-x+3=(x+1)(x+a)+b
则x2-x+3=(x+1)(x+a)+b=x2+ax+x+a+b=x2+(a+1)x+a+b
∵对于任意x上述等式成立
∴$\left\{\begin{array}{l}a+1=-1\\ a+b=3\end{array}\right.$解得:$\left\{\begin{array}{l}a=-2\\ b=5\end{array}\right.$
∴$\frac{{{x^2}-x+3}}{x+1}=\frac{(x+1)(x-2)+5}{x+1}=x-2+\frac{5}{x+1}$
这样,分式$\frac{{{x^2}-x+3}}{x+1}$就拆分成一个整式x-2与一个分式$\frac{5}{x+1}$的和的形式.
(1)将分式$\frac{{{x^2}+6x-3}}{x-1}$拆分成一个整式与一个分式(分子为整数)的和的形式为$x+7+\frac{4}{x-1}$;
(2)已知整数x使分式$\frac{{2{x^2}+5x-20}}{x-3}$的值为整数,则满足条件的整数x=4、16、2、-10;
(3)当-1<x<1时,求分式$\frac{{{x^4}+3{x^2}-2}}{{{x^2}+1}}$的最小值.
分析 (1)仿照例题,列出方程组,求出a、b的值,把原式拆分成一个整式与一个分式(分子为整数)的和的形式;
(2)仿照例题,列出方程组,求出a、b的值,把原式拆分成一个整式与一个分式(分子为整数)的和的形式,根据整除运算解答;
(3)仿照例题,列出方程组,求出a、b的值,把原式拆分成一个整式与一个分式(分子为整数)的和的形式,根据偶次方的非负性解答.
解答 解:(1)由分母x-1,可设x2+6x-3=(x-1)(x+a)+b
则x2+6x-3=(x-1)(x+a)+b=x2+ax-x+a-b=x2+(a-1)x-a+b
∵对于任意x上述等式成立,
∴$\left\{\begin{array}{l}{a-1=6}\\{-a+b=-3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=7}\\{b=4}\end{array}\right.$,
$\frac{{{x^2}+6x-3}}{x-1}$拆分成$x+7+\frac{4}{x-1}$,
故答案为:$x+7+\frac{4}{x-1}$;
(2)由分母x-3,可设2x2+5x-20=(x-3)(2x+a)+b
则2x2+5x-20=(x-3)(2x+a)+b=2x2+ax-6x-3a+b=2x2+(a-6)x-3a+b
∵对于任意x上述等式成立,
$\left\{\begin{array}{l}{a-6=5}\\{-3a+b=-20}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=11}\\{b=13}\end{array}\right.$,
$\frac{{2{x^2}+5x-20}}{x-3}$拆分成2x+11+$\frac{13}{x-3}$,
则满足条件的整数x=4、16、2、-10,
故答案为:4、16、2、-10;
(3)由分母x2+1,可设x4+3x2-2=(x2+1)(x2+a)+b
则x4+3x2-2=(x2+1)(x2+a)+b=x4+ax2+x2+a+b=x4+(a+1)x2+a+b
∵对于任意x上述等式成立,
$\left\{\begin{array}{l}{a+1=3}\\{a+b=-2}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{a=2}\\{b=-4}\end{array}\right.$,
∴$\frac{{{x^4}+3{x^2}-2}}{{{x^2}+1}}={x^2}+2-\frac{4}{{{x^2}+1}}$,
当x=0时,这两式之和最小,所以最小值为-2.
点评 本题考查的是分式的混合运算,掌握多项式乘多项式的运算法则、二元一次方程组的解法是解题的关键.

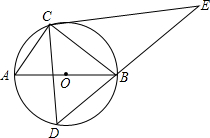 如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=10,AC=6,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )
如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=10,AC=6,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )| A. | $\frac{20}{3}$ | B. | $\frac{40}{3}$ | C. | 16 | D. | $\frac{64}{5}$ |
| A. |  | B. |  | C. |  | D. |  |
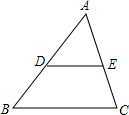 如图,在△ABC中,D、E分别为AB、AC的中点,连接DE,若S△ADE=2,则四边形BDEC的面积为6.
如图,在△ABC中,D、E分别为AB、AC的中点,连接DE,若S△ADE=2,则四边形BDEC的面积为6.