题目内容
3.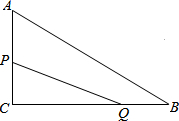 如图,在Rt△ACB中,∠C=90°,AC=6cm,CB=8cm,点P、Q同时由A,B两点出发分别沿AC、BC方向向点C匀速移动,它们的速度都是1cm/s,几秒后△PCQ的面积和四边形APQB的面积相等?
如图,在Rt△ACB中,∠C=90°,AC=6cm,CB=8cm,点P、Q同时由A,B两点出发分别沿AC、BC方向向点C匀速移动,它们的速度都是1cm/s,几秒后△PCQ的面积和四边形APQB的面积相等?
分析 设x秒后△PCQ的面积和四边形APQB的面积相等,即三角形PCQ面积为三角形ABC面积的一半,列出关于x的方程,求出方程的解即可得到结果.
解答 解:设x秒后△PCQ的面积和四边形APQB的面积相等,即S△PCQ=$\frac{1}{2}$S△ABC,
由题意得,AP=BQ=xcm,CP=(6-x)cm,CQ=(8-x)cm,
∴$\frac{1}{2}$(6-x)(8-x)=$\frac{1}{2}$×$\frac{1}{2}$×6×8,
解得:x=2或x=12(不合题意,舍去).
则2s后△PCQ的面积和四边形APQB的面积相等.
点评 此题考查了一元二次方程的应用,找出题中的等量关系是解本题的关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
13.下列方程中是二元一次方程的是( )
| A. | 3x-2y=4z | B. | 6xy+13=0 | C. | 3x=y-1 | D. | $\frac{1}{x}$+3y=2 |
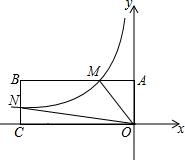 如图,在平面直角坐标系中,矩形OABC的顶点O与坐标原点重合,OC在x轴的负半轴上,OA在y轴的正半轴上,顶点B的坐标为(-6,1).反比例函数y=-$\frac{2}{x}$(x<0)的图象与AB交于点M,与BC交于点N,若点P在y轴上,使S△OMP=S四边形OMBN,则点P的坐标为(0,4)或(0,-4).
如图,在平面直角坐标系中,矩形OABC的顶点O与坐标原点重合,OC在x轴的负半轴上,OA在y轴的正半轴上,顶点B的坐标为(-6,1).反比例函数y=-$\frac{2}{x}$(x<0)的图象与AB交于点M,与BC交于点N,若点P在y轴上,使S△OMP=S四边形OMBN,则点P的坐标为(0,4)或(0,-4).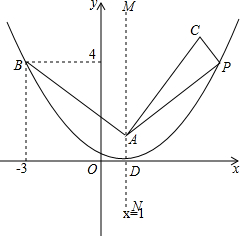 如图,在直角坐标系中,已知点A(1,1)、B(-3,4);将线段BA绕点A顺时针旋转90°得到AC;顶点为D(1,0)抛物线过点B.
如图,在直角坐标系中,已知点A(1,1)、B(-3,4);将线段BA绕点A顺时针旋转90°得到AC;顶点为D(1,0)抛物线过点B.