题目内容
17.已知圆内接正方形的边长为3,则该圆的内接正六边形边长为$\frac{3\sqrt{2}}{2}$.分析 根据已知条件求出该圆的半径,再求出正六边形的边长与外接圆半径相等即可.
解答 解:如图所示:连接OA、OB,OM、OH,
∵四边形ABCD是圆内接正方形,
∴∠AOB=90°;
∵OA=OB,
∴△AOB是等腰直角三角形,
∴∠OBA=45°,
∴AO=AB•sin45°=3×$\frac{\sqrt{2}}{2}$=$\frac{3\sqrt{2}}{2}$,
∵六边形EFGHMN是圆的内接正六边形,
∴∠MOH=$\frac{360°}{6}$=60°,
∵OM=OH,
∴△OMH是等边三角形,
∴MH=OM=OA=$\frac{3\sqrt{2}}{2}$,
即该圆的内接正六边形的边长为$\frac{3\sqrt{2}}{2}$.
故答案为:$\frac{3\sqrt{2}}{2}$.
点评 本题考查了圆的内接正方形与内接正六边形、正方形的性质、正六边形的性质、等腰直角三角形的性质、三角函数、正三角形的性质;由正方形的边长求出圆的半径是解决问题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
7.下列方程中是关于x的一元二次方程的是( )
| A. | x2+$\frac{1}{x}$=0 | B. | x2+3x=x2-1 | C. | (x-1)(x-2)=2 | D. | 3x2-2y=0 |
 一个长方形的纸片,长为a+6,宽为a-1,如图,在长方形纸片的四角剪裁处4个边长为1的正方形,沿着图中虚线折叠成一个无盖长方体纸盒,求纸盒的体积.
一个长方形的纸片,长为a+6,宽为a-1,如图,在长方形纸片的四角剪裁处4个边长为1的正方形,沿着图中虚线折叠成一个无盖长方体纸盒,求纸盒的体积.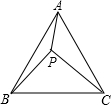 如图,已知点P是等边三角形ABC内一点,PA=4,PB=3,PC=5,求∠APB的度数.
如图,已知点P是等边三角形ABC内一点,PA=4,PB=3,PC=5,求∠APB的度数.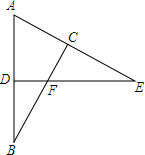 在△ADE中,∠E=22°,延长AD至点B,使得BD=AD,过B点作BC⊥AE,垂足点C,线段BC交边DE于点F,且EF=AB,求∠ADE.
在△ADE中,∠E=22°,延长AD至点B,使得BD=AD,过B点作BC⊥AE,垂足点C,线段BC交边DE于点F,且EF=AB,求∠ADE.