题目内容
9.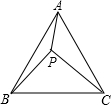 如图,已知点P是等边三角形ABC内一点,PA=4,PB=3,PC=5,求∠APB的度数.
如图,已知点P是等边三角形ABC内一点,PA=4,PB=3,PC=5,求∠APB的度数.
分析 将△BPC绕点B逆时针旋转60°得△BEA,根据旋转的性质得BE=BP=4,AE=PC=5,∠PBE=60°,则△BPE为等边三角形,得到PE=PB=4,∠BPE=60°,在△AEP中,AE=5,AP=3,PE=4,根据勾股定理的逆定理可得到△APE为直角三角形,且∠APE=90°,即可得到∠APB的度数.
解答  解:∵△ABC为等边三角形,
解:∵△ABC为等边三角形,
∴BA=BC,
可将△BPC绕点B逆时针旋转60°得△BEA,
连EP,如图,
∴BE=BP=4,AE=PC=5,∠PBE=60°,
∴△BPE为等边三角形,
∴PE=PB=4,∠BPE=60°,
在△AEP中,AE=5,AP=3,PE=4,
∴AE2=PE2+PA2,
∴△APE为直角三角形,且∠APE=90°,
∴∠APB=90°+60°=150°.
点评 本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.也考查了等边三角形的判定与性质以及勾股定理的逆定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.某自行车厂计划一周生产自行车2100辆,平均每天生产300辆,但由于种种原因,实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产记为正,减产记为负):
(1)根据上表记录的数据,可知该厂星期五生产自行车290辆;
(2)根据上表记录的数据,可知该厂本周实际共生产自行车2108辆;
(3)产量最多的一天比产量最少的一天多生产自行车26辆;
(4)该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖25元;少生产一辆扣30元,那么该厂工人这一周的工资总额是多少元?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +5 | -2 | -4 | +12 | -10 | +16 | -9 |
(2)根据上表记录的数据,可知该厂本周实际共生产自行车2108辆;
(3)产量最多的一天比产量最少的一天多生产自行车26辆;
(4)该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖25元;少生产一辆扣30元,那么该厂工人这一周的工资总额是多少元?
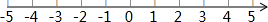 已知数轴上的点A到原点的距离$\sqrt{5}$.-$\sqrt{2}$对应数轴上的点B.
已知数轴上的点A到原点的距离$\sqrt{5}$.-$\sqrt{2}$对应数轴上的点B.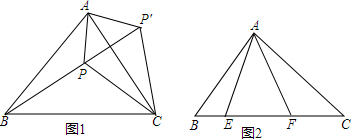
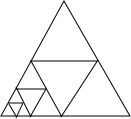 如图,在三角形中的一个最小单元(第一次是大三角形本身)内画三条线段将其分割成四等份,当进行到第15次的时候,图中共61个三角形;当进行到第n次的时候,图中共有多少个三角形?
如图,在三角形中的一个最小单元(第一次是大三角形本身)内画三条线段将其分割成四等份,当进行到第15次的时候,图中共61个三角形;当进行到第n次的时候,图中共有多少个三角形? 如图所示,在一幅长为80cm,宽为50cm的矩形风景画的四周镶一条相同宽度的金色纸边,制成一幅矩形挂图,如果要使整个挂图的面积是5400cm2,求金色纸边的宽为xcm,求出长和宽各是多少?
如图所示,在一幅长为80cm,宽为50cm的矩形风景画的四周镶一条相同宽度的金色纸边,制成一幅矩形挂图,如果要使整个挂图的面积是5400cm2,求金色纸边的宽为xcm,求出长和宽各是多少?