题目内容
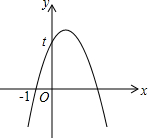 已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,t).
已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,t).(1)当t=3时①求出b,c的值,并写出此二次函数的解析式;
②判断(-2,-5)是否在这个函数的图象上;
③根据图象,写出去图象在第一象限时,自变量x的取值范围.
(2)当对称轴在y轴的右侧时,请写出t的取值范围.
考点:抛物线与x轴的交点
专题:
分析:根据题意得到:b-c=-1,c=t,故y=-x2+(t-1)x+t.
(1)当t=3时,①直接求出y=-x2+2x+3.②运用验证法即可解决问题.③求出抛物线与x轴的交点,借助函数的图象,即可解决问题.
(2)运用对称轴公式,列出不等式即可解决问题.
(1)当t=3时,①直接求出y=-x2+2x+3.②运用验证法即可解决问题.③求出抛物线与x轴的交点,借助函数的图象,即可解决问题.
(2)运用对称轴公式,列出不等式即可解决问题.
解答: 解:∵抛物线y=-x2+bx+c与x轴交于点(-1,0),
解:∵抛物线y=-x2+bx+c与x轴交于点(-1,0),
与y轴的交点坐标为(0,t),
∴b-c=-1,c=t;
∴y=-x2+(t-1)x+t.
(1)当t=3时,
①y=-x2+2x+3.
②∵当x=-2时,y=-5,
∴点(-2,-5)在这个函数的图象上.
③∵当y=0时,-x2+2x+3=0,
解得:x=-1或3,
∴当图象在第一象限时,自变量x的取值范围是0<x<3.
(2)由题意知:y═-x2+(t-1)x+t,
∵对称轴在y轴的右侧,
∴-
>0,解得:t>1.
即当对称轴在y轴的右侧时,t的取值范围是t>1.
 解:∵抛物线y=-x2+bx+c与x轴交于点(-1,0),
解:∵抛物线y=-x2+bx+c与x轴交于点(-1,0),与y轴的交点坐标为(0,t),
∴b-c=-1,c=t;
∴y=-x2+(t-1)x+t.
(1)当t=3时,
①y=-x2+2x+3.
②∵当x=-2时,y=-5,
∴点(-2,-5)在这个函数的图象上.
③∵当y=0时,-x2+2x+3=0,
解得:x=-1或3,
∴当图象在第一象限时,自变量x的取值范围是0<x<3.
(2)由题意知:y═-x2+(t-1)x+t,
∵对称轴在y轴的右侧,
∴-
| t-1 |
| -2 |
即当对称轴在y轴的右侧时,t的取值范围是t>1.
点评:该题主要考查了抛物线与x轴的交点及其性质的应用问题;解题的关键是灵活运用抛物线的性质,数形结合,来分析、判断、推理或解答.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
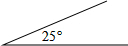 如图,某人沿着坡角为25°的斜坡走了500m,他上升的高度h为( )米.
如图,某人沿着坡角为25°的斜坡走了500m,他上升的高度h为( )米.| A、500sin25° | ||
| B、500cos25° | ||
| C、500tan25° | ||
D、
|
下列命题的逆命题是真命题的是( )
| A、如果两个角都是直角,那么这两个角相等 |
| B、如果三角形中有一个角是直角,那么另外两个角都是锐角 |
| C、全等三角形的三条边对应相等 |
| D、关于某一条直线对称的两个三角形全等 |
 一辆汽车和一辆摩托车分别从A,B两地去C地,它们离A地的路程随时间变化的图象如图所示.则当汽车到达C地时,摩托车距离C地的路程为( )
一辆汽车和一辆摩托车分别从A,B两地去C地,它们离A地的路程随时间变化的图象如图所示.则当汽车到达C地时,摩托车距离C地的路程为( )| A、140km | B、40km |
| C、60km | D、45km |
 如图,在△ABC中,∠C=90°,AB的中垂线交AB于点D,交BC于点E,连接AE,若∠BED=70°,则∠CAE的度数为( )
如图,在△ABC中,∠C=90°,AB的中垂线交AB于点D,交BC于点E,连接AE,若∠BED=70°,则∠CAE的度数为( )| A、30° | B、40° |
| C、50° | D、60° |

