题目内容
在Rt△ABC中,∠C=90°, ,把这个直角三角形绕顶点C旋转后得到Rt△A'B'C,其中点B' 正好落在AB上,A'B'与AC相交于点D,那么
,把这个直角三角形绕顶点C旋转后得到Rt△A'B'C,其中点B' 正好落在AB上,A'B'与AC相交于点D,那么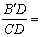 .
.

 .
.
【解析】作CH⊥AB于H,如图,

在Rt△ABC中,∠C=90°,cosB= ,设BC=3x,则AB=5x,AC=
,设BC=3x,则AB=5x,AC= =4x,
=4x,
在Rt△HBC中,cosB= ,而BC=3x,∴BH=
,而BC=3x,∴BH= x,
x,
∵Rt△ABC绕顶点C旋转后得到Rt△A′B′C,其中点B′正好落在AB上,
∴CA′=CA=4x,CB′=CB,∠A′=∠A,∵CH⊥BB′,∴B′H=BH= x,∴AB′=AB-B′H-BH=
x,∴AB′=AB-B′H-BH= x,∵∠ADB′=∠A′DC,∠A′=∠A,∴△ADB′∽△A′DC,∴AB’:A′C =B’D:DC ,即
x,∵∠ADB′=∠A′DC,∠A′=∠A,∴△ADB′∽△A′DC,∴AB’:A′C =B’D:DC ,即 x:4x =B′D:DC ,∴
x:4x =B′D:DC ,∴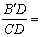
 .
.

练习册系列答案
相关题目

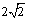 B.
B.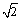 C.
C. D.
D.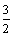
 (单位:千米)与所用时间
(单位:千米)与所用时间 (单位:小时)的函数图象.已知公共汽车比出租车晚1小时出发,到达济南后休息2小时,然后按原路原速返回,结果比出租车最后一次返回沂源早1小时.
(单位:小时)的函数图象.已知公共汽车比出租车晚1小时出发,到达济南后休息2小时,然后按原路原速返回,结果比出租车最后一次返回沂源早1小时.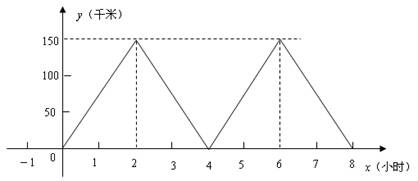
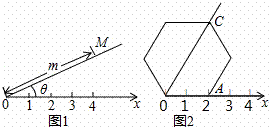
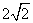 ) D.(50°,
) D.(50°, 与⊙O在第一象限内交于P、Q 两点,分别过P、Q两点向x轴和y轴作垂线,已知点P坐标为(1,3),则图中阴影部分的面积为 .
与⊙O在第一象限内交于P、Q 两点,分别过P、Q两点向x轴和y轴作垂线,已知点P坐标为(1,3),则图中阴影部分的面积为 .

 点M在不同位置时,k的取值会相应变化,点N的个数情况可能会改变,请直接写出点N所有不同的个数情况以及相应的k的取值范围.
点M在不同位置时,k的取值会相应变化,点N的个数情况可能会改变,请直接写出点N所有不同的个数情况以及相应的k的取值范围.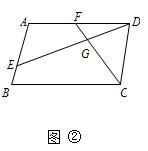
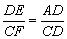 ;
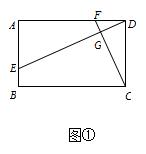
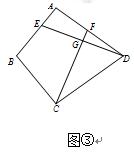
; 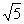 ,∠BAD=90°,DE⊥CF,试求
,∠BAD=90°,DE⊥CF,试求 的值.
的值. 恰好只有5个正整数解,则m的取值范围是 。
恰好只有5个正整数解,则m的取值范围是 。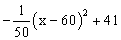 (万元)。当地政府拟规划加快开
(万元)。当地政府拟规划加快开 发该特产的销售,其规划方案为:在规划前后对该项目每年最多可投人100万元的销售投资,在实施规划5年的前两
发该特产的销售,其规划方案为:在规划前后对该项目每年最多可投人100万元的销售投资,在实施规划5年的前两 年中,每
年中,每 在外地销售的投资收益为:每投入
在外地销售的投资收益为:每投入 万元,可获利润Q=
万元,可获利润Q= (万元)。
(万元)。 (2)若按规划实施,求5年所获利润(扣除修路后)的最大值是多少?
(2)若按规划实施,求5年所获利润(扣除修路后)的最大值是多少?