题目内容
某山区的一种特产由于运输原因,长期只能在当地销售,当地政府对该特产的销售投资收益为:每投入x万元,可获得利润P=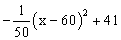 (万元)。当地政府拟规划加快开
(万元)。当地政府拟规划加快开 发该特产的销售,其规划方案为:在规划前后对该项目每年最多可投人100万元的销售投资,在实施规划5年的前两
发该特产的销售,其规划方案为:在规划前后对该项目每年最多可投人100万元的销售投资,在实施规划5年的前两 年中,每
年中,每 年都从100万元
年都从100万元 中拨出60万元用于修建一条公路,两年修成,通车前该特产只能在当地销售;公路通车后的3年中,该特产既在本地销售,也在外地销售。
中拨出60万元用于修建一条公路,两年修成,通车前该特产只能在当地销售;公路通车后的3年中,该特产既在本地销售,也在外地销售。 在外地销售的投资收益为:每投入
在外地销售的投资收益为:每投入 万元,可获利润Q=
万元,可获利润Q= (万元)。
(万元)。
(1)若不进行开发,求5年所获利润的最大值是多少?
 (2)若按规划实施,求5年所获利润(扣除修路后)的最大值是多少?
(2)若按规划实施,求5年所获利润(扣除修路后)的最大值是多少?
(3)根据(1)、(2),该方案是否具有实施价值?
1)∵每投入 万元,可获得利润P=
万元,可获得利润P=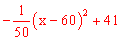 (万元),
(万元),
∴当 =60时,所获利润最大,最大值为41万元。
=60时,所获利润最大,最大值为41万元。
∴若不进行开发,5年所获利润的最大值是:41×5=205(万元)。
(2)前两年:0≤ ≤40,此时因为P随
≤40,此时因为P随 的增大而增大,
的增大而增大,
所以 =40时,P值最大,
=40时,P值最大,
即这两年的获利最大为:2×[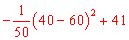 ]=66(万元)。
]=66(万元)。
后三 年:设每年获利
年:设每年获利 ,设当地投资额为
,设当地投资额为 ,则外地投资额为100-
,则外地投资额为100- ,
,
∴ =P+Q=[
=P+Q=[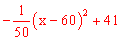 ]+[
]+[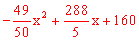 ]
]
=﹣ 2+60
2+60 +129=﹣(
+129=﹣( ﹣30)2+1029。
﹣30)2+1029。
∴当 =30时,y最大且为1029。
=30时,y最大且为1029。
∴这三年的 获利最大为1029×3=3087(万元)
获利最大为1029×3=3087(万元) 。
。
∴5年所获利润(扣除修路后)的最大值是:66 +3087﹣50×2
+3087﹣50×2 =3153(万元)。
=3153(万元)。
(3)规划后5年总利润为3153万元,不实施规划方案仅为205万元,故具有很大的实施价值。
【考点】二次函数的应用(利润问题)。


练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
 ,把这个直角三角形绕顶点C旋转后得到Rt△A'B'C,其中点B' 正好落在AB上,A'B'与AC相交于点D,那么
,把这个直角三角形绕顶点C旋转后得到Rt△A'B'C,其中点B' 正好落在AB上,A'B'与AC相交于点D,那么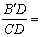 .
.
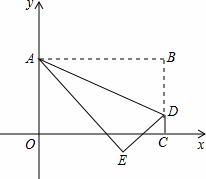
 ,动点P从点A出发,沿折线AD-DC-CB以每秒1个单位长
,动点P从点A出发,沿折线AD-DC-CB以每秒1个单位长 的速度运动到点B停止.设运动时间为t秒,y = S△EPF,则y与t的函数关系式为 。
的速度运动到点B停止.设运动时间为t秒,y = S△EPF,则y与t的函数关系式为 。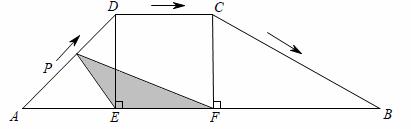
 D。
D。
 bx+1与x轴只有一个交点,且过点A(m,n),B(m+4,n),则n=
bx+1与x轴只有一个交点,且过点A(m,n),B(m+4,n),则n=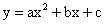
 过点B。
过点B。 、M、N,线段MN的垂直平分线l过点C,交线段OA于点F。当AF=1时,求抛物线的解析式。
、M、N,线段MN的垂直平分线l过点C,交线段OA于点F。当AF=1时,求抛物线的解析式。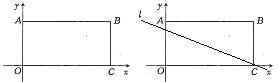
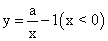 的图象如图,那么关于x的分式方程
的图象如图,那么关于x的分式方程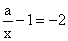 的解是【 】
的解是【 】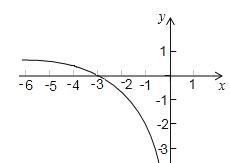
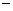 1 B.x=
1 B.x= BP=
BP= 

 OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E,当△ADE是等腰直角三角形时,m=
OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E,当△ADE是等腰直角三角形时,m= ,点E的坐标为 ;
,点E的坐标为 ;