题目内容
已知△ABC的顶点在直角坐标系内的坐标是A(0,2),B(2
,0),C(m,1),△ABC的面积为4
,求m的值.
| 3 |
| 3 |
考点:坐标与图形性质,三角形的面积
专题:计算题
分析:直线y=1与AB交于点D,如图,先利用待定系数法求出直线AB的解析式为y=-
x+2,再可确定D点坐标为(
,1),然后根据三角形面积公式和△ABC的面积=△ACD的面积+△BCD的面积得到
•1•|
-m|+
•1•|
-m|=4
,再解关于m的方程即可.
| ||
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
解答:解: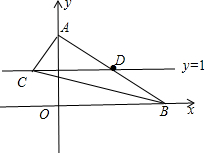 直线y=1与AB交于点D,如图,
直线y=1与AB交于点D,如图,
设直线AB的解析式为y=kx+b,
把A(0,2),B(2
,0)代入得
,
解得
.
所以直线AB的解析式为y=-
x+2,
当y=1时,-
x+2=1,解得x=
,则D点坐标为(
,1),
因为△ABC的面积=△ACD的面积+△BCD的面积,
所以
•1•|
-m|+
•1•|
-m|=4
,即|
-m|=4
,
所以m=5
或-3
.
 直线y=1与AB交于点D,如图,
直线y=1与AB交于点D,如图,设直线AB的解析式为y=kx+b,
把A(0,2),B(2
| 3 |
|
解得
|
所以直线AB的解析式为y=-
| ||
| 3 |
当y=1时,-
| ||
| 3 |
| 3 |
| 3 |
因为△ABC的面积=△ACD的面积+△BCD的面积,
所以
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
所以m=5
| 3 |
| 3 |
点评:本题考查了坐标与图形性质:利用点的坐标特征计算相应的线段长和判断线段与坐标轴的位置关系;记住各象限内点的坐标特征和坐标上点的坐标特征.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
 如图,AB为⊙O直径,直线MN交⊙O于C、D两点,AE⊥MN于E,BF⊥MN于F.
如图,AB为⊙O直径,直线MN交⊙O于C、D两点,AE⊥MN于E,BF⊥MN于F. 一家电信公司给顾客提供两种上网收费方式:
一家电信公司给顾客提供两种上网收费方式: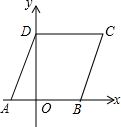 如图所示,将一张边长为4的菱形纸片ABCD固定在一个建立了平面直角坐标系的木板上,A、B在x轴上,D在y轴的正半轴上,C在第一象限,∠BAD=60°.
如图所示,将一张边长为4的菱形纸片ABCD固定在一个建立了平面直角坐标系的木板上,A、B在x轴上,D在y轴的正半轴上,C在第一象限,∠BAD=60°.