题目内容
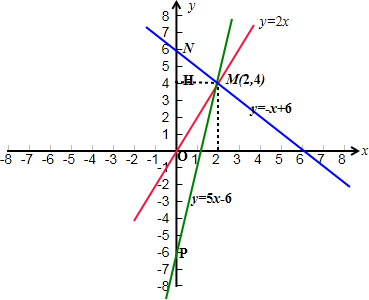
已知正比例函数和一次函数的图象都过点M(2,4),且正比例函数的图象,一次函数的图象与y轴围成的面积为6,求正比例函数和一次函数的解析式.
考点:两条直线相交或平行问题
专题:
分析:设正比例函数关系式为:y=kx,将M(2,4)代入即可求出正比例函数关系式为:y=2x;设:一次函数关系式为:y=kx+b,分两种情况:①当k>0,②当k<0.然后结合图象解答.
解答:解:设正比例函数关系式为:y=kx,
将M(2,4)代入y=kx,得:
2k=4,
所以k=2,
所以正比例函数关系式为:y=2x;
设一次函数关系式为:y=kx+b,
①当k>0时,可画图象,
此时,正比例函数的图象,一次函数的图象与y轴围成△MOP,
∵△MOP的面积=6,
∴
OP•MH=6,
即:
OP•2=6,
∴OP=6,
∵点P在y轴的负半轴上,∴点P(0,-6),
将M(2,4),P(0,-6),分别代入y=kx+b得:
,
解得:
,
∴一次函数关系式为:y=5x-6;
②当k<0时,可画图象,
此时,正比例函数的图象,一次函数的图象与y轴围成△MON,
∵△MON的面积=6,
∴
ON•MH=6,
即:
ON•2=6,
∴ON=6,
∵点P在y轴的正半轴上,∴点P(0,6),
将M(2,4),P(0,6),分别代入y=kx+b得:
,
解得:
,
∴一次函数关系式为:y=-x+6;
综上述正比例函数关系式为:y=2x;
一次函数关系式为:y=5x-6或y=-x+6.
将M(2,4)代入y=kx,得:
2k=4,
所以k=2,
所以正比例函数关系式为:y=2x;
设一次函数关系式为:y=kx+b,
①当k>0时,可画图象,
此时,正比例函数的图象,一次函数的图象与y轴围成△MOP,
∵△MOP的面积=6,
∴
| 1 |
| 2 |
即:
| 1 |
| 2 |
∴OP=6,
∵点P在y轴的负半轴上,∴点P(0,-6),
将M(2,4),P(0,-6),分别代入y=kx+b得:
|
解得:
|
∴一次函数关系式为:y=5x-6;
②当k<0时,可画图象,
此时,正比例函数的图象,一次函数的图象与y轴围成△MON,
∵△MON的面积=6,
∴
| 1 |
| 2 |
即:
| 1 |
| 2 |
∴ON=6,
∵点P在y轴的正半轴上,∴点P(0,6),
将M(2,4),P(0,6),分别代入y=kx+b得:
|
解得:
|
∴一次函数关系式为:y=-x+6;
综上述正比例函数关系式为:y=2x;
一次函数关系式为:y=5x-6或y=-x+6.

点评:此题考查了求正比例函数关系式和一次函数关系式,解题的关键求一次函数关系式分k>0,和k<0两种情况.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 如图,直线CD是线段AB的垂直平分线,P为直线CD上一点,若△PAB的周长为
如图,直线CD是线段AB的垂直平分线,P为直线CD上一点,若△PAB的周长为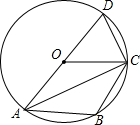 如图,四边形ABCD的四个顶点都在⊙O上,圆心O在AD上,OC∥AB.
如图,四边形ABCD的四个顶点都在⊙O上,圆心O在AD上,OC∥AB.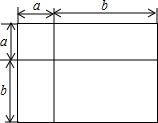 如图,你能根据图形推导出一个什么样的结论?
如图,你能根据图形推导出一个什么样的结论? 为了预防“流感”,某学校对教室用药熏进行消毒,已知药物燃烧时,室内每立方米的空气中含药量y(毫克)与时间x(分)成正比例,药物燃烧后,y与x成反比例,且测得药物8分钟燃毕,此时室内空气中每立方米的含药量为6毫克,请根据题中所提供的信息,解答下列问题:
为了预防“流感”,某学校对教室用药熏进行消毒,已知药物燃烧时,室内每立方米的空气中含药量y(毫克)与时间x(分)成正比例,药物燃烧后,y与x成反比例,且测得药物8分钟燃毕,此时室内空气中每立方米的含药量为6毫克,请根据题中所提供的信息,解答下列问题: