题目内容
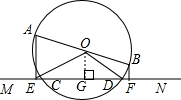
 如图,AB为⊙O直径,直线MN交⊙O于C、D两点,AE⊥MN于E,BF⊥MN于F.
如图,AB为⊙O直径,直线MN交⊙O于C、D两点,AE⊥MN于E,BF⊥MN于F.(1)求证:CE=DF;
(2)若MN向上平移,与AB相交于点P,如果其他条件不变,那么(1)是否仍成立?
考点:垂径定理,勾股定理,梯形中位线定理
专题:计算题
分析:(1)过点O作OG⊥CD于G,如图,根据垂径得CG=DG,然后证明OG为梯形ABFE的中位线,得到GE=GF,于是有CE=DF;
(2)过点O作OG⊥CD于G,根据垂径定理得CG=DG,由于AE⊥EF,OG⊥EF,BF⊥EF,得到AE∥OG∥BF,根据平行线等分线段定理得到GC=GD,则CG-EG=DG-FG,即CE=DF.
(2)过点O作OG⊥CD于G,根据垂径定理得CG=DG,由于AE⊥EF,OG⊥EF,BF⊥EF,得到AE∥OG∥BF,根据平行线等分线段定理得到GC=GD,则CG-EG=DG-FG,即CE=DF.
解答:(1)证明:过点O作OG⊥CD于G,如图,则CG=DG,
∵AE⊥EF,OG⊥EF,BF⊥EF,
∴AE∥OG∥BF,
∵OA=OB,
∴OG为梯形ABFE的中位线,
∴GE=GF,
∴EG-CG=FG-DG,
即CE=DF;
(2)解:(1)中的结论仍成立.理由如下:
过点O作OG⊥CD于G,则CG=DG,
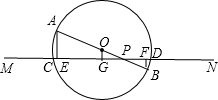
∵AE⊥EF,OG⊥EF,BF⊥EF,
∴AE∥OG∥BF,GC=GD,
∴EG=FG,
∴CG-EG=DG-FG,
即CE=DF.
∵AE⊥EF,OG⊥EF,BF⊥EF,
∴AE∥OG∥BF,
∵OA=OB,
∴OG为梯形ABFE的中位线,
∴GE=GF,
∴EG-CG=FG-DG,
即CE=DF;

(2)解:(1)中的结论仍成立.理由如下:
过点O作OG⊥CD于G,则CG=DG,

∵AE⊥EF,OG⊥EF,BF⊥EF,
∴AE∥OG∥BF,GC=GD,
∴EG=FG,
∴CG-EG=DG-FG,
即CE=DF.
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了梯形的中位线定理.

练习册系列答案
相关题目
下列选项的图形中,不一定是轴对称图形的是( )
| A、线段 | B、等腰三角形 |
| C、直角三角形 | D、圆 |
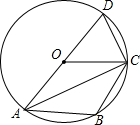 如图,四边形ABCD的四个顶点都在⊙O上,圆心O在AD上,OC∥AB.
如图,四边形ABCD的四个顶点都在⊙O上,圆心O在AD上,OC∥AB.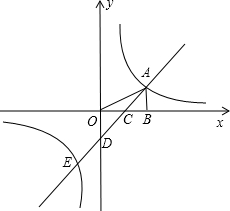 如图,在平面直角坐标系中,点A是反比例函数y1=
如图,在平面直角坐标系中,点A是反比例函数y1= 如图,你能根据图形推导出一个什么样的结论?
如图,你能根据图形推导出一个什么样的结论? 为了预防“流感”,某学校对教室用药熏进行消毒,已知药物燃烧时,室内每立方米的空气中含药量y(毫克)与时间x(分)成正比例,药物燃烧后,y与x成反比例,且测得药物8分钟燃毕,此时室内空气中每立方米的含药量为6毫克,请根据题中所提供的信息,解答下列问题:
为了预防“流感”,某学校对教室用药熏进行消毒,已知药物燃烧时,室内每立方米的空气中含药量y(毫克)与时间x(分)成正比例,药物燃烧后,y与x成反比例,且测得药物8分钟燃毕,此时室内空气中每立方米的含药量为6毫克,请根据题中所提供的信息,解答下列问题: