题目内容
5.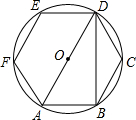 如图,正六边形ABCDEF内接于⊙O,连接AD、BD,则∠DAB的余弦值是$\frac{1}{2}$.
如图,正六边形ABCDEF内接于⊙O,连接AD、BD,则∠DAB的余弦值是$\frac{1}{2}$.
分析 连接OB,根据正六边形的性质得到∠AOB=60°,得到△AOB是等边三角形,根据60°的余弦值是$\frac{1}{2}$解答即可.
解答 解: 连接OB,
连接OB,
∵六边形ABCDEF是正六边形,
∴∠AOB=60°,
∵OA=OB,
∴△AOB是等边三角形,
∴∠DAB=60°,
∵cos60°=$\frac{1}{2}$,
∴∠DAB的余弦值是$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题考查的是正多边形和圆、特殊角的三角函数值,掌握正多边形的中心角的计算公式、熟记特殊角的三角函数值是解题的关键.

练习册系列答案
相关题目
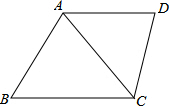 如图,梯形ABCD中,AD∥BC,AC为对角线,且∠DCA=∠B,线段AD、BC的长是方程x(x-4)+2(4-x)=0的两根,且AD<BC,CD=3,求AB与AC的长.
如图,梯形ABCD中,AD∥BC,AC为对角线,且∠DCA=∠B,线段AD、BC的长是方程x(x-4)+2(4-x)=0的两根,且AD<BC,CD=3,求AB与AC的长. 节约能源,保护生态,迎接低碳时代的到来,某纸品加工厂利用边角线裁出正方形和长方形两种硬纸片,制作甲、乙两种无盖的长方体纸盒出售给礼品店.
节约能源,保护生态,迎接低碳时代的到来,某纸品加工厂利用边角线裁出正方形和长方形两种硬纸片,制作甲、乙两种无盖的长方体纸盒出售给礼品店. 如图,点E在?ABCD的边AD上,沿BE折叠,点A落在边CD上的点F处,若△FDE的周长为8,△FCB的周长为22.求FC的长.
如图,点E在?ABCD的边AD上,沿BE折叠,点A落在边CD上的点F处,若△FDE的周长为8,△FCB的周长为22.求FC的长.