题目内容
13.平移抛物线M1:y=ax2+c得到抛物线M2,抛物线M2经过抛物线 M1的顶点 A,抛物线M2的对称轴分别交抛物线M1,M2于B,C两点,若点C的坐标为(2,c-5),则△ABC 的面积为10.分析 由y=ax2+c变换后顶点坐标(2,c-5),可得 M2的解析式,根据A在M2上,可得a,求出BC,即可得到答案.
解答 解:由题意,得
M2的解析式为y=a(x-2)2+c-5,
由A在M2上,得4a+c-5=c,
解得a=$\frac{5}{4}$,
C(2,c-5),B(2,5+c).
BC=5+c-(c-5)=10.
S△ABC=$\frac{1}{2}$×2×10=10,
故答案为:10.
点评 本题考查了二次函数图象与几何变换,利用待定系数法求得a的值是解题关键,还利用了平移的知识:左加右减,上加下减.

练习册系列答案
相关题目
1.目前节能灯在城市已基本普及,某商场计划购进甲、乙两种节能灯共1200只,这两种节能灯的进价、售价如下表:
(1)如何进货,进货款恰好为46000元?
(2)为确保乙型节能灯顺利畅销,在(1)的条件下,商家决定对乙型节能灯进行打折出售,且全部售完后,乙型节能灯的利润率为20%,请问乙型节能灯需打几折?
| 进价(元/只) | 售价(元/只) | |
| 甲型 | 25 | 30 |
| 乙型 | 45 | 60 |
(2)为确保乙型节能灯顺利畅销,在(1)的条件下,商家决定对乙型节能灯进行打折出售,且全部售完后,乙型节能灯的利润率为20%,请问乙型节能灯需打几折?
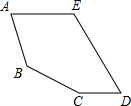 聪聪用五根宽度相同的木条拼成了一个五边形,如图所示,已知AE∥CD,∠A=$\frac{1}{2}$∠C,∠B=120°,∠D=50°.
聪聪用五根宽度相同的木条拼成了一个五边形,如图所示,已知AE∥CD,∠A=$\frac{1}{2}$∠C,∠B=120°,∠D=50°.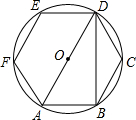 如图,正六边形ABCDEF内接于⊙O,连接AD、BD,则∠DAB的余弦值是$\frac{1}{2}$.
如图,正六边形ABCDEF内接于⊙O,连接AD、BD,则∠DAB的余弦值是$\frac{1}{2}$.