题目内容
18. 如图,已知在△ABC中,∠B与∠C的平分线交于点P.当∠BPC=118°时,则∠A的度数为56°.
如图,已知在△ABC中,∠B与∠C的平分线交于点P.当∠BPC=118°时,则∠A的度数为56°.
分析 据三角形的内角和等于180°,求出∠PBC+∠PCB的度数,再根据角平分线的定义,求得∠ABC+∠ACB.在△ABC中,根据三角形内角和定理,即可求出∠BAC的度数.
解答 解:在△PBC中,∵∠BPC=118°,
∴∠PBC+∠PCB=180°-118°=62°.
∵PB、PC分别是∠ABC和∠ACB的角平分线,
∴∠ABC+∠ACB=2(∠PBC+∠PCB)=2×62°=124°,
在△ABC中,∠A=180°-(∠ABC+∠ACB)=180°-124°=56°.
故答案为:56°.
点评 本题主要考查了利用三角形的内角和定理和角平分线的定义求解,熟练掌握定理和角平分线的定义是解题的关键.

练习册系列答案
相关题目
13.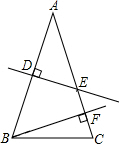 如图,已知在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,CE的垂直平分线正好经过点B,与AC相交于点F,求∠A的度数是( )
如图,已知在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,CE的垂直平分线正好经过点B,与AC相交于点F,求∠A的度数是( )
 如图,已知在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,CE的垂直平分线正好经过点B,与AC相交于点F,求∠A的度数是( )
如图,已知在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,CE的垂直平分线正好经过点B,与AC相交于点F,求∠A的度数是( )| A. | 30° | B. | 35° | C. | 45° | D. | 36° |
 如图,△ABC中,边AB的中垂线分别交BC、AB于点D、E,AE=3cm,△ABC的周长为18cm,则△ADC的周长是12 cm.
如图,△ABC中,边AB的中垂线分别交BC、AB于点D、E,AE=3cm,△ABC的周长为18cm,则△ADC的周长是12 cm.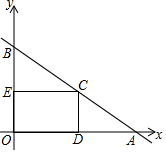 如图,平面直角坐标系中,直线AB与x轴,y轴分别交于A(6,0),B(0,3)两点,点C为线段AB上的一动点,过点C作CD⊥x轴于点D.
如图,平面直角坐标系中,直线AB与x轴,y轴分别交于A(6,0),B(0,3)两点,点C为线段AB上的一动点,过点C作CD⊥x轴于点D.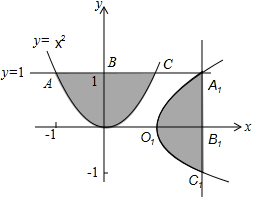 如图,把抛物线y=x2与直线y=1围成的图形OABC绕原点O顺时针旋转90°后,再沿x轴向右平移1个单位得到图形O1A1B1C1.
如图,把抛物线y=x2与直线y=1围成的图形OABC绕原点O顺时针旋转90°后,再沿x轴向右平移1个单位得到图形O1A1B1C1.