题目内容
10.有一列数,第一个记作a1,第二个记作a2,…,第n个记作an,若an+1(1+$\frac{1}{{a}_{n}}$)=1,当a1=1时,求a1a2+a2a3+a3a4+…+a2015a2016的值.分析 已知等式整理得到关系式,把原式变形即可求出值.
解答 解:已知等式整理得:an+1=$\frac{{a}_{n}}{{a}_{n}+1}$,
当n=1时,a2=$\frac{1}{2}$,a3=$\frac{1}{3}$,a4=$\frac{1}{4}$,…,an=$\frac{1}{n}$,
则原式=$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2015×2016}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{2015}$-$\frac{1}{2016}$=1-$\frac{1}{2016}$=$\frac{2015}{2016}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.当用配方法解一元二次方程x2-3=4x时,下列方程变形正确的是( )
| A. | (x-2)2=2 | B. | (x-2)2=4 | C. | (x-2)2=1 | D. | (x-2)2=7 |

 如图,已知在△ABC中,∠B与∠C的平分线交于点P.当∠BPC=118°时,则∠A的度数为56°.
如图,已知在△ABC中,∠B与∠C的平分线交于点P.当∠BPC=118°时,则∠A的度数为56°.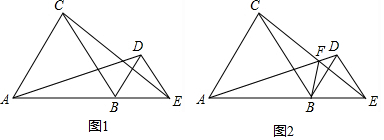

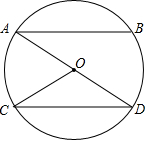 如图,AD是⊙O的直径,AB∥CD,$\widehat{AC}$的度数为60°,则∠BAD的度数为30°.
如图,AD是⊙O的直径,AB∥CD,$\widehat{AC}$的度数为60°,则∠BAD的度数为30°.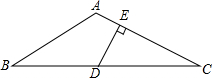 如图,△ABC中,AB=AC,∠BAC=120°,D为BC的中点,DE⊥AC于E,AE=1,求CE的长.
如图,△ABC中,AB=AC,∠BAC=120°,D为BC的中点,DE⊥AC于E,AE=1,求CE的长.