题目内容
12.求下列各式的值:(1)已知x=$\sqrt{3}+1$,y=$\sqrt{3}-1$,求x2+2xy+y2的值;
(2)已知x=$\sqrt{2}-1$,求x2+3x-1的值.
分析 (1)由x=$\sqrt{3}+1$,y=$\sqrt{3}-1$,得出x+y=2$\sqrt{3}$,进一步把代数式利用完全平方公式因式分解,代入求得答案即可;
(2)首先把x2+3x-1化为(x+1)2+x-2,再进一步代入求得数值即可.
解答 解:(1)∵x=$\sqrt{3}+1$,y=$\sqrt{3}-1$,
∴x+y=2$\sqrt{3}$,
∴x2+2xy+y2=(x+y)2=12;
(2)∵x=$\sqrt{2}-1$,
∴x2+3x-1=(x+1)2+x-2=2+$\sqrt{2}$-1-2=$\sqrt{2}$-1.
点评 此题考查二次根式的化简求值,先利用完全平方公式因式分解,再进一步代入使计算简单易行.

练习册系列答案
相关题目
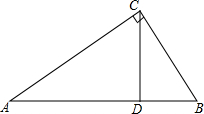 如图,△ABC中,∠ACB=90°,AB=$\sqrt{8}$,BC=$\sqrt{2}$.
如图,△ABC中,∠ACB=90°,AB=$\sqrt{8}$,BC=$\sqrt{2}$.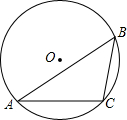 如图,⊙O是△ABC的外接圆,BC=4cm,∠A=30°,求⊙O的面积(用两种不同的方法求解).
如图,⊙O是△ABC的外接圆,BC=4cm,∠A=30°,求⊙O的面积(用两种不同的方法求解). 如图,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=57°,求∠CAD的度数.
如图,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=57°,求∠CAD的度数.