题目内容
 如图,在四边形ABCD中,AB=AC,∠BAC+∠BDC=180°,CE∥DB交AD于E,探究线段EC与DC的数量关系.
如图,在四边形ABCD中,AB=AC,∠BAC+∠BDC=180°,CE∥DB交AD于E,探究线段EC与DC的数量关系.考点:圆周角定理
专题:
分析:EC=DC.利用⊙O是四边形ABCD的外接圆的性质和已知条件AB=AC推知∠ADB=∠ADC;再结合平行线的性质、等量代换推知∠ADC=∠DEC,则EC=DC.
解答: 解:EC=DC.理由如下:
解:EC=DC.理由如下:
∵∠BAC+∠BDC=180°,
∴A、B、D、C四点共圆,
又∵AB=AC,
∴
=
,
∴∠ADB=∠ADC,
又∵CE∥DB,
∴∠ADB=∠DEC,
∴∠ADC=∠DEC,
∴EC=DC.
 解:EC=DC.理由如下:
解:EC=DC.理由如下:∵∠BAC+∠BDC=180°,
∴A、B、D、C四点共圆,
又∵AB=AC,
∴
 |
| AB |
 |
| AC |
∴∠ADB=∠ADC,
又∵CE∥DB,
∴∠ADB=∠DEC,
∴∠ADC=∠DEC,
∴EC=DC.
点评:本题考查了圆周角定理.此题根据“对角互补的四边形内接于圆”证得A、B、D、C四点共圆是解题的关键.

练习册系列答案
相关题目
下列说法错误的是( )
| A、角的平分线是一条射线 |
| B、线段的垂直平分线是一条直线 |
| C、角的对称轴是它的角平分线 |
| D、线段的对称轴是它的中垂线 |
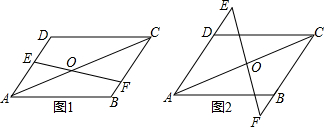
 在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A逆时针旋转到△AED的位置,使得CE∥AB,则∠DAB等于
在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A逆时针旋转到△AED的位置,使得CE∥AB,则∠DAB等于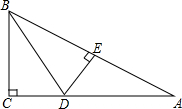 如图所示,在△ABC中,∠C=90°,BD平分∠ABC交AC于点D,作DE⊥AB于点E.若△BCD与△ABC的面积之比为3:8,求△ADE与△ABC的面积之比.
如图所示,在△ABC中,∠C=90°,BD平分∠ABC交AC于点D,作DE⊥AB于点E.若△BCD与△ABC的面积之比为3:8,求△ADE与△ABC的面积之比.