题目内容
要使等式(2-
x)2+
=0成立,x的值是 .
| 1 |
| 3 |
| ||
| x-4 |
考点:非负数的性质:算术平方根,非负数的性质:偶次方
专题:
分析:先根据二次根式性质开出来,再分为x>4和x<4两个情况讨论,解方程即可.
解答:解:∵等式(2-
x)2+
=0成立,
∴(2-
x)2+
=0,
①当x>4时,方程化为(2-
x)2+1=0,
(2-
x)2=-1,
此方程无解;
②当x<4时,方程化为(2-
x)2-1=0,
(2-
x)2=1,
2-
x=±1,
x1=3,x2=9,
故答案为:3或9.
| 1 |
| 3 |
| ||
| x-4 |
∴(2-
| 1 |
| 3 |
| |x-4| |
| x-4 |
①当x>4时,方程化为(2-
| 1 |
| 3 |
(2-
| 1 |
| 3 |
此方程无解;
②当x<4时,方程化为(2-
| 1 |
| 3 |
(2-
| 1 |
| 3 |
2-
| 1 |
| 3 |
x1=3,x2=9,
故答案为:3或9.
点评:本题考查了二次根式的性质,解一元二次方程的应用,注意要进行分类讨论.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
 如图,以A、B、C、D、O作为线段的端点,共有线段( )
如图,以A、B、C、D、O作为线段的端点,共有线段( )| A、6条 | B、8条 |
| C、10条 | D、12条 |
 在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A逆时针旋转到△AED的位置,使得CE∥AB,则∠DAB等于
在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A逆时针旋转到△AED的位置,使得CE∥AB,则∠DAB等于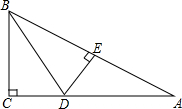 如图所示,在△ABC中,∠C=90°,BD平分∠ABC交AC于点D,作DE⊥AB于点E.若△BCD与△ABC的面积之比为3:8,求△ADE与△ABC的面积之比.
如图所示,在△ABC中,∠C=90°,BD平分∠ABC交AC于点D,作DE⊥AB于点E.若△BCD与△ABC的面积之比为3:8,求△ADE与△ABC的面积之比.