题目内容
已知抛物线y=ax2+bx+c(a>0),过点(1,0)和(0,-2),且对称轴在y轴左侧,设p=a-b,则p的取值范围为 .
考点:二次函数图象与系数的关系
专题:
分析:由抛物线y=ax2+bx+c过(0,-2)得出c=-2,由对称轴在y轴左侧且过点(1,0),得出y=ax2+bx-2与x轴的另一交点在x=-1的左侧,a+b-2=0,那么当x=-1时y<0,即a-b-2<0,p<2.再将b=2-a代入p=a-b得到p=2a-2,由a>0,利用不等式的性质得出p>-2,由此得到p的取值范围是-2<p<2.
解答:解:∵抛物线y=ax2+bx+c过(0,-2),
∴c=-2,y=ax2+bx-2.
∵对称轴在y轴左侧,且过点(1,0),
∴y=ax2+bx-2与x轴的另一交点在x=-1的左侧,a+b-2=0,
∴当x=-1时y<0,
即a-b-2<0,
∴a-b<2,
∴p<2.
∵a+b-2=0,
∴b=2-a,
∴p=a-b=a-(2-a)=2a-2,
∵a>0,
∴p=2a-2>-2,
∴p的取值范围为-2<p<2.
故答案为-2<p<2.
∴c=-2,y=ax2+bx-2.
∵对称轴在y轴左侧,且过点(1,0),
∴y=ax2+bx-2与x轴的另一交点在x=-1的左侧,a+b-2=0,
∴当x=-1时y<0,
即a-b-2<0,
∴a-b<2,
∴p<2.
∵a+b-2=0,
∴b=2-a,
∴p=a-b=a-(2-a)=2a-2,
∵a>0,
∴p=2a-2>-2,
∴p的取值范围为-2<p<2.
故答案为-2<p<2.
点评:本题考查了二次函数图象与系数的关系,二次函数图象上点的坐标特征,二次函数的性质,不等式的性质,难度适中.得出y=ax2+bx-2与x轴的另一交点在x=-1的左侧是解题的关键.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
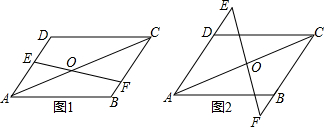
 如图,以A、B、C、D、O作为线段的端点,共有线段( )
如图,以A、B、C、D、O作为线段的端点,共有线段( )| A、6条 | B、8条 |
| C、10条 | D、12条 |
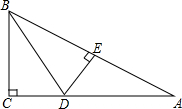 如图所示,在△ABC中,∠C=90°,BD平分∠ABC交AC于点D,作DE⊥AB于点E.若△BCD与△ABC的面积之比为3:8,求△ADE与△ABC的面积之比.
如图所示,在△ABC中,∠C=90°,BD平分∠ABC交AC于点D,作DE⊥AB于点E.若△BCD与△ABC的面积之比为3:8,求△ADE与△ABC的面积之比.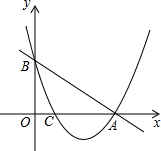 如图,直线y=-x+3交x轴于点A,交y轴于点B,抛物线经过A、B、C三点.点C的坐标为(1,0).
如图,直线y=-x+3交x轴于点A,交y轴于点B,抛物线经过A、B、C三点.点C的坐标为(1,0).