题目内容
8.(1)若(2x-1)10=a0+a1x+a2x2+…+a10x10,求a1+a3+a5+a7+a9及a2+a4+a6+a8+a10的值.(2)若(x-1)4(x+2)5=a0+a1x+a2x2+…+a9x9,求a1+a3+a5+a7+a9及a2+a4+a6+a8的值.
分析 (1)令x=0,x=1,x=-1,x=0分别代入式子(2x-1)10=a0+a1x+a2x2+…+a10x10中,将相应的结果再进行加减运算即可求得答案.
(2)令x=0,x=1,x=-1,x=0分别代入式子(x-1)4(x+2)5=a0+a1x+a2x2+…+a9x9中,将相应的结果再进行加减运算即可求得答案.
解答 解:(1)令x=0,得
(-1)10=a0
∴a0=1
令x=1,得
(2×1-1)10=a0+a1+a2+a3+a4+a5+a6+a7+a8+a9+a10
,即:a0+a1+a2+a3+a4+a5+a6+a7+a8+a9+a10=1 ①
令x=-1,得
[2×(-1)-1]10=a0-a1+a2-a3+a4-a5+a6-a7+a8-a9+a10
即:a0-a1+a2-a3+a4-a5+a6-a7+a8-a9+a10=(-3)10 ②
①-②,得
2(a1+a3+a5+a7+a9)=1-(-3)10
∴a1+a3+a5+a7+a9=$\frac{1-(-3)^{10}}{2}$
①+②,得
2(a0+a2+a4+a6+a8+a10)=1+(-3)10
又∵a0=1
∴a2+a4+a6+a8+a10=$\frac{(-3)^{10}-1}{2}$
(2)令x=0,得
(0-1)4(0+2)5=a0
即a0=32
当x=1时,得
(1-1)4(1+2)5=a0+a1+a2+a3+a4+a5+a6+a7+a8+a9
即:a0+a1+a2+a3+a4+a5+a6+a7+a8+a9=0 ①
当x=-1时,得
(-1-1)4(-1+2)5=a0-a1+a2-a3+a4-a5+a6-a7+a8-a9
即:a0-a1+a2-a3+a4-a5+a6-a7+a8-a9=24 ②
①-②,得
2(a1+a3+a5+a7+a9)=-24
∴a1+a3+a5+a7+a9=-8
①+②,得
2(a0+a2+a4+a6+a8)=24
又∵a0=32
∴a2+a4+a6+a8=-24
点评 本题考查对式子的赋值变形,巧妙运算,最终求的问题的答案.

 如图,点O是两个同心圆的圆心,大圆半径OA,OB交小圆于点C,D.下列结论中正确的个数有( )
如图,点O是两个同心圆的圆心,大圆半径OA,OB交小圆于点C,D.下列结论中正确的个数有( )①∠OCD=∠OAB;②AB=CD;③$\widehat{AB}$=$\widehat{CD}$.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
| A. | $\sqrt{13}$ | B. | 13 | C. | $\sqrt{13}$或$\sqrt{5}$ | D. | $\sqrt{13}$或3 |
| A. | 95° | B. | 15° | C. | 95°或15° | D. | 170°或30° |
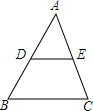 如图,△ABC中,DE∥BC,AD=6,AC=8,BD=AE,求BD的长.
如图,△ABC中,DE∥BC,AD=6,AC=8,BD=AE,求BD的长. 如图所示草地,BC=4m,AB与CD的长均大于6m,现有一只拴在B点的羊在草地上活动,栓羊的绳子长6m,请画出羊的活动区域.
如图所示草地,BC=4m,AB与CD的长均大于6m,现有一只拴在B点的羊在草地上活动,栓羊的绳子长6m,请画出羊的活动区域.