题目内容
14.如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形.(a>0)剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙)则矩形的面积为( )
| A. | (2a2+5a)cm2 | B. | (3a+15)cm2 | C. | (6a+9)cm2 | D. | (6a+15)cm2 |
分析 利用大正方形的面积减去小正方形的面积即可,解题时注意平方差公式的运用.
解答 解:长方形的面积为:
(a+4)2-(a+1)2
=(a+4+a+1)(a+4-a-1)
=3(2a+5)
=6a+15(cm2).
答:矩形的面积是(6a+15)cm2.
故选:D.
点评 此题考查了平方差公式的几何背景,图形的剪拼,关键是根据题意列出式子,运用平方公式进行计算,要熟记公式.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
5.关于x的方程2x+4=3m和x-1=m有相同的解,则m的值是( )
| A. | 6 | B. | 5 | C. | $\frac{5}{2}$ | D. | -$\frac{2}{3}$ |
9.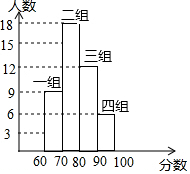 某校七(3)班的同学进行了一次安全知识测试,测试成绩进行整理后分成四个组,并绘制如图所示的频数直方图,则第二组的频数是( )
某校七(3)班的同学进行了一次安全知识测试,测试成绩进行整理后分成四个组,并绘制如图所示的频数直方图,则第二组的频数是( )
 某校七(3)班的同学进行了一次安全知识测试,测试成绩进行整理后分成四个组,并绘制如图所示的频数直方图,则第二组的频数是( )
某校七(3)班的同学进行了一次安全知识测试,测试成绩进行整理后分成四个组,并绘制如图所示的频数直方图,则第二组的频数是( )| A. | 0.4 | B. | 18 | C. | 0.6 | D. | 27 |
6.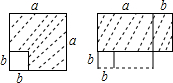 如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成为一个矩形,通过计算两个图形(阴影部分)的面积,可以验证的等式是( )
如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成为一个矩形,通过计算两个图形(阴影部分)的面积,可以验证的等式是( )
 如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成为一个矩形,通过计算两个图形(阴影部分)的面积,可以验证的等式是( )
如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成为一个矩形,通过计算两个图形(阴影部分)的面积,可以验证的等式是( )| A. | (a+2b)(a-b)=a2+ab-2b2 | B. | (a+b)2=a2+2ab+b2 | ||
| C. | (a-b)2=a2-2ab+b2 | D. | a2-b2=(a+b)(a-b) |
3. 如图,在△ABC中,DE∥BC,若AD=5,BD=10.AE=3,则CE=( )
如图,在△ABC中,DE∥BC,若AD=5,BD=10.AE=3,则CE=( )
 如图,在△ABC中,DE∥BC,若AD=5,BD=10.AE=3,则CE=( )
如图,在△ABC中,DE∥BC,若AD=5,BD=10.AE=3,则CE=( )| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
4.下列说法不正确的是( )
| A. | 1的平方根是±1 | B. | -1的立方根是-1 | ||
| C. | $\sqrt{16}$的算术平方根是2 | D. | $\sqrt{8}$是最简二次根式 |
 如图所示,同位角有a对,内错角有b对,同旁内角有c对,则a+b+c的值是14.
如图所示,同位角有a对,内错角有b对,同旁内角有c对,则a+b+c的值是14.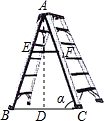 如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα=$\frac{5}{2}$,则“人字梯”的顶端离地面的高度AD是180cm.
如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα=$\frac{5}{2}$,则“人字梯”的顶端离地面的高度AD是180cm.