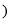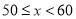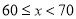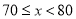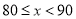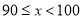题目内容
数轴上表示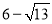 的点
的点 的位置应在( ).
的位置应在( ).
A. 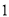 与
与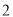 之间 B.
之间 B. 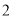 与
与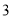 之间 C.
之间 C. 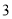 与
与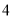 之间 D.
之间 D. 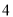 与
与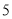 之间
之间
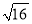 的平方根是 ( )
的平方根是 ( )
A. 4 B. 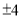 C.
C. 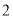 D.
D. 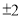
备受世界瞩目的世纪工程“港珠澳大桥”总造价约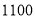 亿人民币,用科学记数法表示( ).
亿人民币,用科学记数法表示( ).
A. 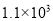 元 B.
元 B. 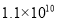 元 C.
元 C. 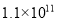 元 D.
元 D. 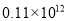 元
元
下列计算正确的是( ).
A. 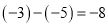 B.
B. 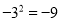 C.
C. 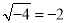 D.
D. 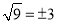
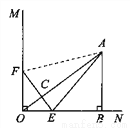
如图,已知∠MON=90º,A是∠MON内部的一点,过点A作AB⊥ON,垂点为点B,AB=3厘米,OB=4厘米,动点E、F同时从O点出发,点E以1.5厘米/秒的速度沿ON方向运动,点F以2厘米/秒的速度沿OM方向运动,EF与OA交于点C,连接AE,当点E到达点B时,点F随之停止运动。设运动时间为t秒(t>0)。
(1)当t=1秒时,ΔEOF与ΔABO是否相似?请说明理由。
(2)在运动过程中,不论t取何值时,总有EF⊥OA,为什么?
(3)连接AF,在运动过程中,是否存在某一时刻t,使得SΔAEF=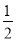 S四边形ABOF ?若存在,请求出此时t的值;若不存在,请说明理由。
S四边形ABOF ?若存在,请求出此时t的值;若不存在,请说明理由。
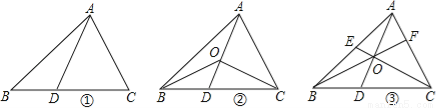
如图,在△ABC中,D是BC边上的点(不与点B、C重合),连结AD.
问题引入:
(1)如图①,当点D是BC边上的中点时,S△ABD:S△ABC= ;当点D是BC边上任意一点时,S△ABD:S△ABC= (用图中已有线段表示).
探索研究:
(2)如图②,在△ABC中,O点是线段AD上一点(不与点A、D重合),连结BO、CO,试猜想S△BOC与S△ABC之比应该等于图中哪两条线段之比,并说明理由.
拓展应用:
(3)如图③,O是线段AD上一点(不与点A、D重合),连结BO并延长交AC于点F,连结CO并延长交AB于点E,试猜想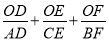 的值,并说明理由.
的值,并说明理由.
- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
下列事件中,属于必然事件的是( )
A.二次函数的图象是抛物线
B.任意一个一元二次方程都有实数根
C.三角形的外心在三角形的外部
D.投掷一枚均匀的硬币100次,正面朝上的次数为50次
A 【解析】 试题分析:利用三角形外心的定义以及二次函数图象的性质以及随机事件的定义分析得出即可. 【解析】 A、二次函数的图象是抛物线,正确,是必然事件; B、任意一个一元二次方程都有实数根,是随机事件,故此选项错误; C、三角形的外心在三角形的外部,错误; D、投掷一枚均匀的硬币100次,正面朝上的次数为50次,是随机事件,故此选项错误; 故选:A....下列图形中,既是轴对称图形又是中心对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
下列关于x的方程中,一定是一元二次方程的是( )
A. (m﹣3)x2﹣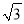 x﹣2 B. k2x+5k+6=0; C.
x﹣2 B. k2x+5k+6=0; C.  x2﹣
x2﹣ x﹣
x﹣ =0; D. 3x2+
=0; D. 3x2+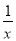 ﹣2=0
﹣2=0
抛物线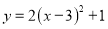 的顶点坐标是( )
的顶点坐标是( )
A. (3, 1) B. (3,-1) C. (-3, 1) D. (-3, -1)
查看答案解下列方程
(1)(x+1)2﹣9=0
(2)(x﹣1)3=8.
查看答案怎样才能把一行树苗栽直?请你想出办法,并说明其中的道理.
查看答案 试题属性- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣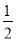 ,y2)、点C(
,y2)、点C(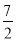 ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
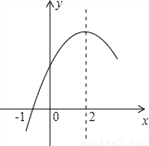
A. 2个 B. 3个 C. 4个 D. 5个
B 【解析】试题分析:由﹣=2,可得4a+b=0.故(1)正确;当x=﹣3时,y<0,所以9a﹣3b+c<0,即9a+c<3b,故(2)错误;由图象可知抛物线经过(﹣1,0)和(5,0),可得,解得,所以8a+7b+2c=8a﹣28a﹣10a=﹣30a,又因a<0,所以8a+7b=2c>0,故(3)正确.已知点A(﹣3,y1)、点B(﹣,y2)、点C(,y3),计算﹣2=,2﹣(﹣)=,因<...如图,将△ABC绕着点C按顺时针方向旋转20°,B点落在B′位置,A点落在A′位置,若AC⊥A′B′,则∠BAC的度数是( )
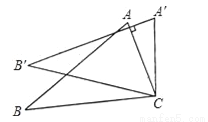
A. 50° B. 60° C. 70° D. 80°
查看答案关于x的一元二次方程x2﹣6x+2k=0有两个不相等的实数根,则实数k的取值范围是( )
A. k≤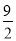 B. k<
B. k<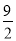 C. k≥
C. k≥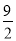 D. k>
D. k>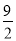
抛物线y=﹣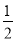 x2﹣x的顶点坐标是( )
x2﹣x的顶点坐标是( )
A. (1,﹣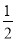 ) B. (﹣1,
) B. (﹣1, 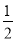 ) C. (
) C. (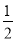 ,﹣1) D. (1,0)
,﹣1) D. (1,0)
4张扑克牌如图(1)所示放在桌子上,小敏把其中两张旋转180°后得到如图(2)所示,那么她所旋转的牌从左起是( )

A.第一张、第二张
B.第二张、第三张
C.第三张、第四张
D.第四张、第一张
查看答案已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:
| … |
| 0 | 1 | 3 | … |
| … |
| 1 | 3 | 1 | … |
则下列判断中正确的是( )
A. 抛物线开口向上 B. 抛物线与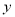 轴交于负半轴
轴交于负半轴
C. 当x=4时,y>0 D. 方程ax2+bx+c=0的正根在3与4之间
查看答案 试题属性- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
已知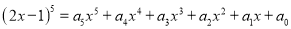 是关于
是关于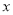 的恒等式,则
的恒等式,则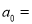 __________.且
__________.且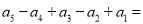 __________.
__________.
若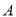 与
与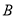 都是三次多项式,
都是三次多项式, 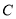 是五次多项式,有下列说法:①
是五次多项式,有下列说法:①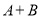 可能是六次多项式;②
可能是六次多项式;②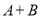 一定是次数不高于三次的整式;③
一定是次数不高于三次的整式;③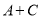 一定五次多项式;④
一定五次多项式;④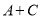 一定是五次整式;⑤
一定是五次整式;⑤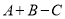 可能是常数.其中正确的是__________.
可能是常数.其中正确的是__________.
已知有理数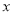 ,
, 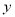 满足:
满足: 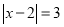 ,
, 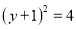 且
且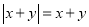 ,则
,则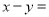 __________.
__________.
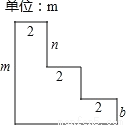
如图是一个摆放礼物的柜子截面的示意图,每一个转角都是直角,数据如图所示.则该图形的周长为__________.面积为__________.(用含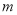 ,
, 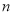 ,
, 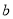 的代数式表示化简后的结果)
的代数式表示化简后的结果)
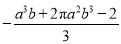 是__________次__________项式,常数项为__________.
是__________次__________项式,常数项为__________.
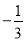 的倒数是__________;
的倒数是__________; 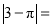 __________.
__________.
- 题型:填空题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
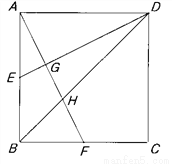
如图,在△ABC中,D是BC边上的点(不与点B、C重合),连结AD.
问题引入:
(1)如图①,当点D是BC边上的中点时,S△ABD:S△ABC= ;当点D是BC边上任意一点时,S△ABD:S△ABC= (用图中已有线段表示).
探索研究:
(2)如图②,在△ABC中,O点是线段AD上一点(不与点A、D重合),连结BO、CO,试猜想S△BOC与S△ABC之比应该等于图中哪两条线段之比,并说明理由.
拓展应用:
(3)如图③,O是线段AD上一点(不与点A、D重合),连结BO并延长交AC于点F,连结CO并延长交AB于点E,试猜想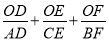 的值,并说明理由.
的值,并说明理由.

如图, 正比例函数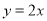 的图象与反比例函数
的图象与反比例函数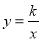 的图象交于A、B两点,过点A作AC垂直x轴于点C,连接BC,若ΔABC面积为 2.
的图象交于A、B两点,过点A作AC垂直x轴于点C,连接BC,若ΔABC面积为 2.
(1)求k的值
(2)x轴上是否存在一点D,使ΔABD是以AB为斜边的直角三角形?若存在,求出点D的坐标,若不存在,说明理由。
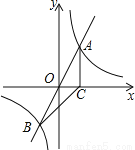
如图是某一蓄水池每1h的排水量V(m3/h)与排完水池中的水所用时间t(h)之间的函数图象。
(1)请你根据图象提供的信息求出此蓄水池的蓄水量;
(2)写出函数的函数表达式;
(3)若要6h排完水池的水,那么每1h的排水量应该是多少?
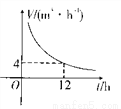
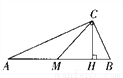
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90º,E为AB的中点,求证:
(1)AC2=AB·AD;
(2)CE∥AD。
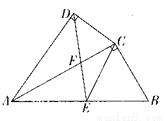
正方形ABCD中,E,F分别是AB与BC边上的中点,连接AF,DE,BD,交于G,H(如图所示)。求AG:GH:HF的值。
如图,△ABC三个顶点坐标分别为A (1,2),B (3,1),C (2,3),以原点O为位似中心,将△ABC放大为原来的2倍得△A′B′C′.
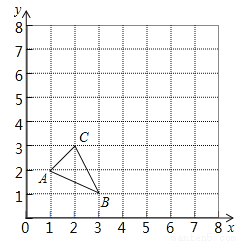
(1)在图中第一象限内画出符合要求的△A′B′C′;(不要求写画法)
(2)△A′B′C′的面积是: .
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
若y与x3成反比例,且x=2时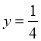 。
。
(1)求y与x的函数表达式;
(2)求y=—16时x的值。
(1)y= (2)x= 【解析】试题分析:(1)根据y与x3成反比例,可设,把x=2, ,代入可得k=2, 即可求出函数表达式,(2)把y=-16代入(1)中函数关系式即可求解. 试题解析:(1)因为y与x3成反比例, 则可设, 因为x=2, , 所以, 所以 (2)当 y=-16时,代入可得: ,解得: x=.如图,点A在双曲线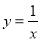 上,点B在双曲线
上,点B在双曲线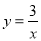 上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为__________.
上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为__________.
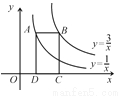
如图所示,冰冰在墙上挂了一面镜子AB,调整好标杆CD,正好通过标杆顶部在镜子上边缘A处看到旗杆的顶端E的影子,已知AB=2m,CD=1.5m,BD=2m,BF=20m,则旗杆EF的高度为__________m。
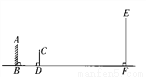
如图,在ΔABC中,∠ACB=90°,AC=7,BC=3,CM、CH 分别是中线和高,则SΔACM:SΔBCM = __________,SΔACH:SΔBCH = __________.
已知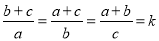 ,则抛物线
,则抛物线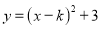 的顶点坐标为____________。
的顶点坐标为____________。
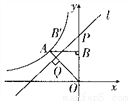
如图,反比例函数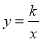 (k<0)的图象经过点A(-1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到了点B’在此反比例函数的图象上,则t的值是( )
(k<0)的图象经过点A(-1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到了点B’在此反比例函数的图象上,则t的值是( )
A. 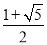 B.
B. 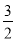 C.
C. 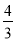 D.
D. 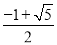
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
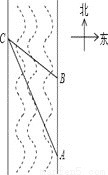
在2014年6月23日第十届保护韩江母亲河徒步节上,如图所示,某同学为了测得一段南北流向的河段的宽,在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西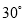 的方向上,沿河岸向北前行40米到达B处,测得C在B北偏西
的方向上,沿河岸向北前行40米到达B处,测得C在B北偏西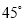 的方向上,请你根据以上数据,求这段河段的宽度
的方向上,请你根据以上数据,求这段河段的宽度 结果保留根号
结果保留根号
为支援雅安灾区,某学校计划用“义捐义卖”活动中筹集的部分资金用于购买A,B两种型号的学习用品共1000件,已知A型学习用品的单价为20元,B型学习用品的单价为30元.
(1)若购买这批学习用品用了26000元,则购买A,B两种学习用品各多少件?
(2)若购买这批学习用品的钱不超过28000元,则最多购买B型学习用品多少件?
查看答案“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数 |
第1组 |
| 6 |
第2组 |
| 8 |
第3组 |
| 14 |
第4组 |
| a |
第5组 |
| 10 |
请结合图表完成下列各题:
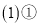 求表中a的值;
求表中a的值; 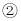 频数分布直方图补充完整;
频数分布直方图补充完整;
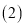 若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
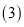 第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
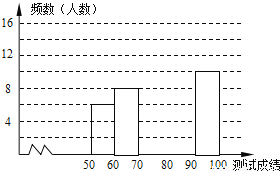
如图,在平面直角坐标系中,一次函数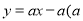 为常数
为常数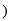 的图象与y轴相交于点A,与函数
的图象与y轴相交于点A,与函数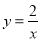 的图象相交于点
的图象相交于点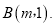
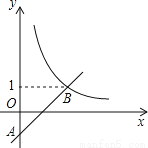
 求点B的坐标及一次函数的解析式;
求点B的坐标及一次函数的解析式;
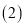 若点P在y轴上,且
若点P在y轴上,且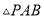 为直角三角形,请直接写出点P的坐标.
为直角三角形,请直接写出点P的坐标.
如图, 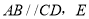 是CD上一点,BE交AD于点
是CD上一点,BE交AD于点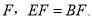 求证:
求证: 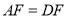 .
.
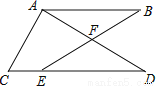
如图,  的底边经过
的底边经过 上的点C,且
上的点C,且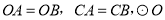 与OA、OB分别交于D、E两点.
与OA、OB分别交于D、E两点.
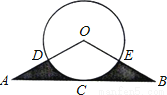
 求证:AB是
求证:AB是 的切线;
的切线;
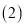 若D为OA的中点,阴影部分的面积为
若D为OA的中点,阴影部分的面积为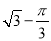 ,求
,求 的半径r.
的半径r.
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图,直线a和b被直线c所截,下列条件能判断a∥b的是( )
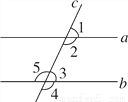
A. ∠1=∠2 B. ∠2=∠3
C. ∠1+∠4=180° D. ∠2+∠5=180°
C 【解析】试题分析:A、∠1和∠2是邻补角,∠1=∠2不能判定a∥b; B、∠2和∠3是同旁内角,∠2=∠3不能判定a∥b; C、∵∠1+∠4=180°,∠1+∠2=180°, ∴∠2=∠4, ∴a∥b; D、∠2和∠5是内错角,∠2+∠5=180°不能判定a∥b. 故选C.下列计算正确的是( )
A. -3x2y·5x2y=2x2y B. -2x2y3·2x3y=-2x5y4
C. 35x3y2÷5x2y=7xy D. (-2x-y)(2x+y)=4x2-y2
查看答案下列说法:①两条直线被第三条直线所截,内错角相等;②相等的角是对顶角;③互余的两个角一定都是锐角;④互补的两个角一定有一个为钝角,另一个角为锐角。其中正确的有( )
A.1个 B.2个 C.3个 D.4个
查看答案下列计算正确的是( )
A.a2+a3=a5 B.a2•a3=a6
C.(a2)3=a5 D.a5÷a2=a3
查看答案在不借助任何工具的情况下,人的眼睛可以看到的最小物体的长度约为0.00003米,将0.00003用科学记数法表示为( )
A. 3×10-5 B. 0.3×10-4 C. 30×10-6 D. 3×105
查看答案用火柴拼成如图所示的几何图形。图1有6根火柴棒拼成,图2有11根火柴棒拼成,图3由16根拼成······

图1 图2 图3
(1)图4由__________根火柴棒拼成;
(2)根据规律猜想,图n由________根火柴棒拼成;(用含n的代数式表示,不用说明理由)
(3)是否存在图x恰好由2017根火柴棒拼成?若存在,求出x的值;若不存在,请说明理由.
查看答案 试题属性- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
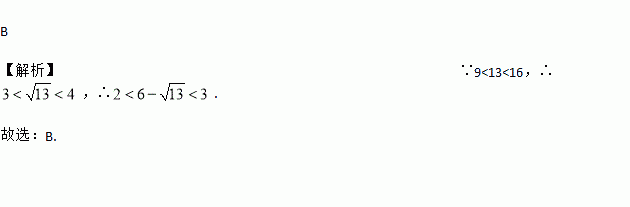

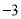
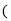 人数
人数