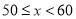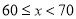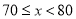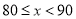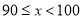��Ŀ����
���㣺 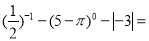 ��
��
��ͼ��ʾ����֪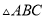 �У�
�У� 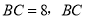 �ϵĸ�
�ϵĸ�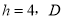 ΪBC��һ�㣬
ΪBC��һ�㣬 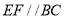 ����AB�ڵ�E����AC�ڵ�
����AB�ڵ�E����AC�ڵ�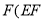 ����A��
����A��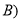 ����E��BC�ľ���Ϊx����
����E��BC�ľ���Ϊx����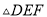 �����y����x�ĺ�����ͼ�����Ϊ
�����y����x�ĺ�����ͼ�����Ϊ ��
��
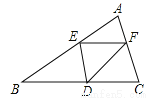
A. 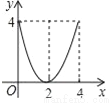 B.
B. 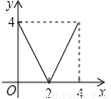
C. 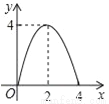 D.
D. 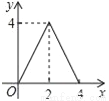
��50���ͺ�ΪL�ij����İ����л�����ͺ�ΪM�ij�����ÿ��20��������ÿ���л����M�ų����������
M�ų����� | 0 | 1 | 4 | 5 | 7 | 9 | 10 | 11 |
���� | 7 | 3 | 10 | 15 | 5 | 4 | 3 | 3 |
�����������ݣ�ѡ����ȷѡ� ��.
A. M�ų���һ����47��
B. �������ȡһ��������L�ų�����������9������¼�
C. �������ȡһ��������L�ų�����������4�ĸ���Ϊ0.26
D. ��50�����������һ�𣬴�������ó�һ��������ǡ����M�ŵĸ���Ϊ0.252
�鿴����ͼ������ABCD���ܳ�Ϊ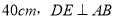 ������Ϊ
������Ϊ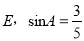 �������н�����ȷ����
�������н�����ȷ����
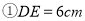 ��
�� 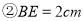 ��
�� 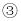 �������Ϊ
�������Ϊ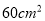 ��
�� 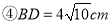 ��
��
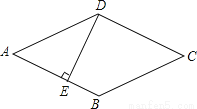
A. 1�� B. 2�� C. 3�� D. 4��
�鿴��Ϊִ�С�������������ߣ�ij��2014��Ͷ���������2500��Ԫ��Ԥ�Ƶ�2016��������ۼ�Ͷ��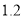 ��Ԫ
��Ԫ ��ÿ��Ͷ��������ѵ���ƽ�������ٷ���Ϊx�������з�����ȷ����
��ÿ��Ͷ��������ѵ���ƽ�������ٷ���Ϊx�������з�����ȷ����
A. 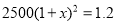
B. 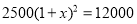
C. 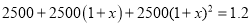
D. 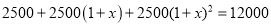
��ͼ��ʾ��ֱ��y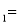 x
x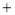 b��y
b��y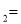 kx
kx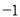 �ཻ�ڵ�P����P�ĺ�����Ϊ
�ཻ�ڵ�P����P�ĺ�����Ϊ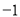 �������x�IJ� ��ʽx
�������x�IJ� ��ʽx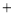 b
b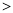 kx
kx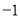 �Ľ⼯�������ϱ�ʾ��ȷ����
�Ľ⼯�������ϱ�ʾ��ȷ����
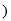
A. 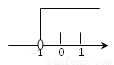
B. 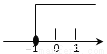
C. 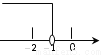
D. 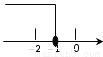
- ���ͣ������
- �Ѷȣ���
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д����κ���y=ax2+bx+c��a��0���IJ���ͼ����ͼ��ʾ��ͼ����㣨��1��0�����Գ���Ϊֱ��x=2�����н��ۣ���1��4a+b=0����2��9a+c��3b����3��8a+7b+2c��0����4������A����3��y1������B����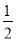 ��y2������C��
��y2������C��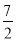 ��y3���ڸú���ͼ���ϣ���y1��y3��y2����5��������a��x+1����x��5��=��3������Ϊx1��x2����x1��x2����x1����1��5��x2��������ȷ�Ľ����У�������
��y3���ڸú���ͼ���ϣ���y1��y3��y2����5��������a��x+1����x��5��=��3������Ϊx1��x2����x1��x2����x1����1��5��x2��������ȷ�Ľ����У�������
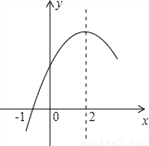
A. 2�� B. 3�� C. 4�� D. 5��
B ������������������ɩ�=2���ɵ�4a+b=0���ʣ�1����ȷ����x=��3ʱ��y��0������9a��3b+c��0����9a+c��3b���ʣ�2��������ͼ���֪�����߾�������1��0���ͣ�5��0�����ɵã���ã�����8a+7b+2c=8a��28a��10a=��30a������a��0������8a+7b=2c��0���ʣ�3����ȷ����֪��A����3��y1������B������y2������C����y3�������㩁2=��2��������=����...��ͼ������ABC���ŵ�C��˳ʱ�뷽����ת20�㣬B������B��λ�ã�A������A��λ�ã���AC��A��B�䣬���BAC�Ķ����ǣ� ��
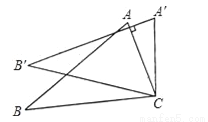
A. 50�� B. 60�� C. 70�� D. 80��
�鿴������x��һԪ���η���x2��6x+2k=0����������ȵ�ʵ��������ʵ��k��ȡֵ��Χ�ǣ� ��
A. k��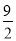 B. k<
B. k<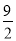 C. k��
C. k��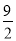 D. k>
D. k>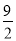
������y=��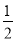 x2��x�Ķ��������ǣ�������
x2��x�Ķ��������ǣ�������
A. ��1����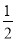 �� B. ����1��
�� B. ����1�� 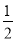 �� C. ��
�� C. ��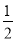 ����1�� D. ��1��0��
����1�� D. ��1��0��
4���˿�����ͼ��1����ʾ���������ϣ�С��������������ת180���õ���ͼ��2����ʾ����ô������ת���ƴ������ǣ� ��

A����һ�š��ڶ���
B���ڶ��š�������
C�������š�������
D�������š���һ��
�鿴����֪���κ���y=ax2+bx+c��y��x�IJ��ֶ�Ӧֵ���±���
| �� |
| 0 | 1 | 3 | �� |
| �� |
| 1 | 3 | 1 | �� |
�������ж�����ȷ���ǣ�������
A. �����߿������� B. ��������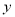 �ύ�ڸ�����
�ύ�ڸ�����
C. ��x��4ʱ��y��0 D. ����ax2+bx+c=0��������3��4֮��
�鿴�� ��������- ���ͣ���ѡ��
- �Ѷȣ���
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
��y��x3�ɷ���������x=2ʱ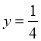 ��
��
��1����y��x�ĺ�������ʽ��
��2����y=��16ʱx��ֵ��
��1��y= ��2��x= ���������������:(1)����y��x3�ɷ�����,����,��x=2, ,����ɵ�k=2, ���������������ʽ,(2)��y=��16����(1)�к�����ϵʽ�������. �������:(1)��Ϊy��x3�ɷ�����, �����, ��Ϊx=2, , ����, ���� (2)�� y=��16ʱ,����ɵ�: ,���: x=.��ͼ����A��˫����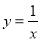 �ϣ���B��˫����
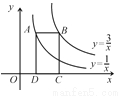
�ϣ���B��˫����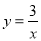 �ϣ���AB��x�ᣬC��D��x���ϣ����ı���ABCDΪ���Σ����������Ϊ__________��
�ϣ���AB��x�ᣬC��D��x���ϣ����ı���ABCDΪ���Σ����������Ϊ__________��
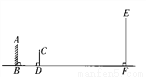
��ͼ��ʾ��������ǽ�Ϲ���һ�澵��AB�������ñ��CD������ͨ����˶����ھ����ϱ�ԵA��������˵Ķ���E��Ӱ�ӣ���֪AB=2m��CD=1.5m��BD=2m��BF=20m�������EF�ĸ߶�Ϊ__________m��
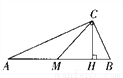
��ͼ���ڦ�ABC�У���ACB=90�㣬AC=7��BC=3��CM��CH �ֱ������ߺߣ���S��ACM��S��BCM = __________��S��ACH��S��BCH = __________.
��֪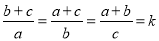 ����������
����������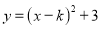 �Ķ�������Ϊ____________��
�Ķ�������Ϊ____________��
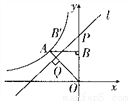
��ͼ������������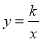 ��k��0����ͼ����A��-1��1��������A��AB��y�ᣬ����ΪB����y�����������ȡһ��P��0��t��������P��ֱ��OA�Ĵ���l����ֱ��lΪ�Գ��ᣬ��B����ԳƱ任�õ��˵�B���ڴ˷�����������ͼ���ϣ���t��ֵ�ǣ� ��
��k��0����ͼ����A��-1��1��������A��AB��y�ᣬ����ΪB����y�����������ȡһ��P��0��t��������P��ֱ��OA�Ĵ���l����ֱ��lΪ�Գ��ᣬ��B����ԳƱ任�õ��˵�B���ڴ˷�����������ͼ���ϣ���t��ֵ�ǣ� ��
A. 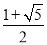 B.
B. 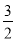 C.
C. 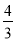 D.
D. 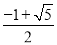
- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
��2014��6��23�յ�ʮ�챣������ĸ��ͽ�����ϣ���ͼ��ʾ��ijͬѧΪ�˲��һ���ϱ�����ĺӶεĿ����ںӶ�����A���۲�Ӷ�ˮ����һ��C�����C��A��ƫ��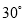 �ķ����ϣ��غӰ���ǰ��40����B�������C��B��ƫ��
�ķ����ϣ��غӰ���ǰ��40����B�������C��B��ƫ��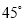 �ķ����ϣ���������������ݣ�����κӶεĿ���
�ķ����ϣ���������������ݣ�����κӶεĿ���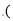 �����������
�����������
Ϊ֧Ԯ�Ű�������ijѧУ�ƻ��á������������гO�IJ����ʽ����ڹ���A��B�����ͺŵ�ѧϰ��Ʒ��1000������֪A��ѧϰ��Ʒ�ĵ���Ϊ20Ԫ��B��ѧϰ��Ʒ�ĵ���Ϊ30Ԫ��
��1������������ѧϰ��Ʒ����26000Ԫ������A��B����ѧϰ��Ʒ�����ټ���
��2������������ѧϰ��Ʒ��Ǯ������28000Ԫ��������B��ѧϰ��Ʒ���ټ���
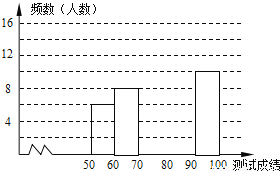
�鿴�������л�ʫ�ʣ�Ѱ�Ļ�����Ʒ����֮������ijУ�ٰ����조�й�ʫ�ʴ�ᡱ����ѡ�κ���50��ѧ���μӾ�������50��ѧ��ͬʱĬд50��ʫ�ʣ���ÿ��ȷĬд��һ��ʫ�ʵ�2�֣����ݲ��Գɼ����Ƴ�����Ƶ���ֲ����Ͳ���Ƶ���ֲ�ֱ��ͼ��ͼ����
��� | �ɼ�x�� | Ƶ�� |
��1�� |
| 6 |
��2�� |
| 8 |
��3�� |
| 14 |
��4�� |
| a |
��5�� |
| 10 |
����ͼ��������и��⣺
 �����a��ֵ��
�����a��ֵ��  Ƶ���ֲ�ֱ��ͼ����������
Ƶ���ֲ�ֱ��ͼ����������
 �����Գɼ�������80��Ϊ���㣬�β��Ե��������Ƕ��٣�
�����Գɼ�������80��Ϊ���㣬�β��Ե��������Ƕ��٣�
 ��5��10��ͬѧ�У���4����ͬѧ���ֽ���10��ͬѧƽ���ֳ�������жԿ���ϰ����4����ͬѧÿ������ˣ���С����Сǿ������ͬѧ�ܷ���ͬһ��ĸ��ʣ�
��5��10��ͬѧ�У���4����ͬѧ���ֽ���10��ͬѧƽ���ֳ�������жԿ���ϰ����4����ͬѧÿ������ˣ���С����Сǿ������ͬѧ�ܷ���ͬһ��ĸ��ʣ�
��ͼ����ƽ��ֱ������ϵ�У�һ�κ���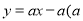 Ϊ����
Ϊ����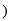 ��ͼ����y���ཻ�ڵ�A���뺯��
��ͼ����y���ཻ�ڵ�A���뺯��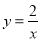 ��ͼ���ཻ�ڵ�
��ͼ���ཻ�ڵ�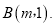
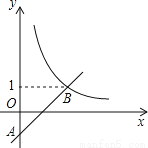
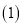 ���B�����꼰һ�κ����Ľ���ʽ��
���B�����꼰һ�κ����Ľ���ʽ��
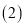 ����P��y���ϣ���
����P��y���ϣ���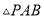 Ϊֱ�������Σ���ֱ��д����P�����꣮
Ϊֱ�������Σ���ֱ��д����P�����꣮
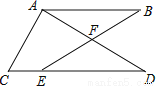
��ͼ�� 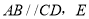 ��CD��һ�㣬BE��AD�ڵ�
��CD��һ�㣬BE��AD�ڵ�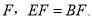 ��֤��
��֤�� 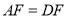 ��
��
��ͼ�� 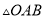 �ĵױ߾���
�ĵױ߾���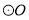 �ϵĵ�C����
�ϵĵ�C����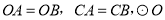 ��OA��OB�ֱ���D��E���㣮
��OA��OB�ֱ���D��E���㣮
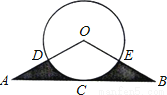
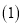 ��֤��AB��
��֤��AB��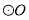 �����ߣ�
�����ߣ�
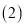 ��DΪOA���е㣬��Ӱ���ֵ����Ϊ
��DΪOA���е㣬��Ӱ���ֵ����Ϊ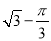 ����
����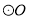 �İ뾶r��
�İ뾶r��
- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
��ͼ��ʾ��ֱ��y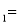 x
x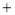 b��y
b��y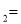 kx
kx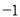 �ཻ�ڵ�P����P�ĺ�����Ϊ
�ཻ�ڵ�P����P�ĺ�����Ϊ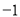 �������x�IJ� ��ʽx
�������x�IJ� ��ʽx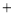 b
b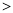 kx
kx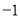 �Ľ⼯�������ϱ�ʾ��ȷ����
�Ľ⼯�������ϱ�ʾ��ȷ����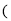

A. 
B. 
C. 
D. 
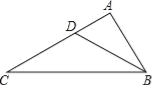
��ͼ����D�ǡ�ABC�ı�AC����һ�㣬�ҡ�ABD=��C�����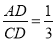 ����ô
����ô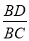 =�� ��
=�� ��
A�� B��
B�� C��
C�� D��
D�� 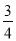
��ͼ��ʾ�ļ�����ĸ���ͼ��
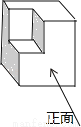
A.  B.
B.  C.
C.  D.
D. 
����������ȷ����
A. 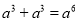 B.
B. 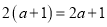 C.
C. 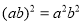 D.
D. 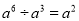
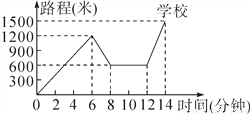
�½������г�ȥ��ѧ���������������ٶ�����һ��·ʱ����Ȼ����Ҫ��ij���飬�������ۻص��վ�����һ����꣬����������ȥѧУ����������������ѧ��·��������ʱ��Ĺ�ϵʾ��ͼ������ͼ���ṩ����Ϣ�ش��������⣺
(1)�½ܼҵ�ѧУ�ľ����Ƕ����ף���굽ѧУ�ľ����Ƕ����ף�
(2)�½������ͣ���˶��ٷ��ӣ�������ѧ;�У��½�һ����ʻ�˶����ף�
(3)��������ѧ��;���ĸ�ʱ��γ½��ﳵ�ٶ���죿�����ٶ��Ƕ����ף�
(4)����½ܲ����飬���������ٶ�ȥѧУ����Ҫ���ٷ��ӣ�������ѧ���������ö��ٷ��ӣ�
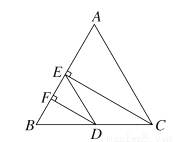
��ͼ����������ABC�У�CE��AB��E��DF��AB��F��AC��ED��CE�ǡ�ACB��ƽ���ߣ��ԱȽϡ�EDF���BDF�Ĵ�С����˵�����ɣ�
- ���ͣ���ѡ��
- �Ѷȣ���
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
��ͼ��ʾ���ó�Ϊ20����˿���ӳ�һ�������Σ��賤���ε�һ��Ϊx�����Ϊy������x�ı仯��y��ֵҲ��֮�仯��
(1)д��y��x֮��Ĺ�ϵʽ����ָ��������仯�У��ĸ����Ա������ĸ����������
(2)�ñ����ʾ��x��1�仯��9ʱ(ÿ������1)��y����Ӧֵ��
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
y |
(3)��xΪ��ֵʱ��y��ֵ���
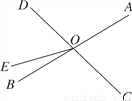
��1��y��10x��x2��x���Ա�����y���������(2)�������������3����xΪ5ʱ��y��ֵ��� �������������������1�������ܳ��ĵ�����ϵ�ɵó����ε���һ��Ϊ10��x����ô�����x(10��x)���Ա�����x��������Ǻ���ֵy�� ��2�������x��ֵ���루1���еĺ�������ʽ��ֵ���ɣ� ��3�����ݣ�2�����õĽ��ۿɵ�xΪ��ֵʱ��y��ֵ��� ��������� �������� ��1����...��ͼ��ֱ��AB��CD�ཻ�ڵ�O��OE�ѡ�BOD�ֳ������֣�
(1)ͼ�С�AOC�ĶԶ���Ϊ________����BOE�IJ���Ϊ________��
(2)����AOC��75�㣬�ҡ�BOE�á�EOD��1��4�����AOE�Ķ�����
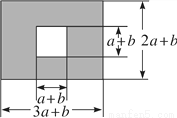
��ͼ��ij����һ�鳤Ϊ(3a��b)�ס���Ϊ(2a��b)�ij����εأ��м佫��һ���߳�Ϊ(a��b)�������ε��滮���żƻ������²��ֽ����̻���
(1)���ú�a��b��ʽ�ӱ�ʾ�̻����ֵ����(���Ҫ����)��
(2)��a��3��b��2��������̻����ֵ������
���㣺
��1��5x(2x2��3x��4)��
��2��20172��2018��2016��
��3��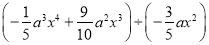 ��
��
��4��(a��b)(a��b)��(a��b)2��2a2.
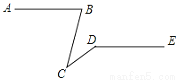
�鿴����ͼ����֪AB��DE����ABC=75�㣬��CDE=150�㣬���BCD�Ķ���Ϊ____��
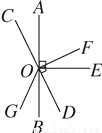
��ͼ��ֱ��AB��ֱ��CD���ڵ�O��OE��AB����DOF��90�㣬OBƽ�֡�DOG�������н��ۣ��ٵ���AOF��60��ʱ����DOE��60�㣻��ODΪ��EOG��ƽ���ߣ������BOD��ȵĽ����������ܡ�COG����AOB��2��EOF.������ȷ�Ľ�����________(�����)��
��
- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
��ͼ��ֱ��a��b��ֱ��c���أ������������ж�a��b����(����)
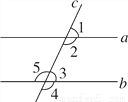
A. ��1����2 B. ��2����3
C. ��1����4��180�� D. ��2����5��180��
C �����������������A����1�͡�2���ڲ��ǣ���1����2�����ж�a��b�� B����2�͡�3��ͬ���ڽǣ���2����3�����ж�a��b�� C���ߡ�1����4��180�㣬��1����2��180�㣬 ���2����4�� ��a��b�� D����2�͡�5���ڴ��ǣ���2����5��180�㲻���ж�a��b�� ��ѡC�����м�����ȷ����(����)
A. ��3x2y��5x2y��2x2y B. ��2x2y3��2x3y����2x5y4
C. 35x3y2��5x2y��7xy D. (��2x��y)(2x��y)��4x2��y2
�鿴������˵����������ֱ�߱�������ֱ�����أ��ڴ�����ȣ�����ȵĽ��ǶԶ��ǣ��ۻ����������һ��������ǣ��ܻ�����������һ����һ��Ϊ�۽ǣ���һ����Ϊ��ǡ�������ȷ���У� ��
A��1�� B��2�� C��3�� D��4��
�鿴�����м�����ȷ���ǣ� ��
A��a2+a3=a5 B��a2•a3=a6
C����a2��3=a5 D��a5��a2=a3
�鿴���ڲ������κι��ߵ�����£��˵��۾����Կ�������С����ij���ԼΪ0.00003�ף���0.00003�ÿ�ѧ��������ʾΪ(����)
A. 3��10��5 B. 0.3��10��4 C. 30��10��6 D. 3��105
�鿴���û��ƴ����ͼ��ʾ�ļ���ͼ�Ρ�ͼ1��6������ƴ�ɣ�ͼ2��11������ƴ�ɣ�ͼ3��16��ƴ�ɡ�����������

ͼ1 ͼ2 ͼ3
��1��ͼ4��__________������ƴ�ɣ�
��2�����ݹ��ɲ��룬ͼn��________������ƴ�ɣ����ú�n�Ĵ���ʽ��ʾ������˵�����ɣ�
��3���Ƿ����ͼxǡ����2017������ƴ�ɣ������ڣ����x��ֵ���������ڣ���˵������.
�鿴�� ��������- ���ͣ���ѡ��
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
����ʽ����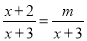 �⣬��m��ֵΪ��������
�⣬��m��ֵΪ��������
A. ��1 B. 0 C. 1 D. 3
A ������������ͬ����(x+3)�ã� x+2=m�� x=m-2�� �߷����� ��x+3=0�� ��m-2+3=0�� ��m=-1�� ��ѡA.��֪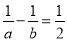 ����
����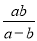 ��ֵΪ��������
��ֵΪ��������
A. 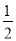 B.
B. 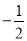 C. ��2 D. 2
C. ��2 D. 2
��ͼ��AB=AD��Ҫ˵����ABC�ա�ADE�������ӵ����������ǣ�������
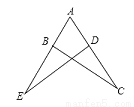
A. ��E=��C B. AC=AE C. ��ADE=��ABC D. DE=BC
�鿴����ͼ���ӱ߳�Ϊa����������ȥ��һ���߳�Ϊb��С�����Σ�Ȼ��ʣ�ಿ�ּ�����ƴ��һ�������Σ�������������֤�ĵ�ʽ�ǣ�������
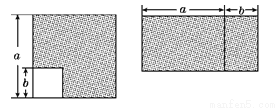
A. ��a��b����a��b����a2��b2 B. ��a��b��2��a2��2ab��b2
C. ��a��b��2��a2��2ab��b2 D. a2��ab��a��a��b��
�鿴�������ʽ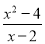 ��ֵ����0����ô�� ��
��ֵ����0����ô�� ��
A. 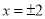 B.
B. 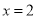 C.
C. 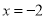 D.
D. 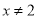
����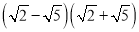 �Ľ���ǣ�������
�Ľ���ǣ�������
A. ��3 B. 3 C. 7 D. 4
�鿴�� ��������- ���ͣ���ѡ��
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������


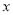
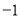
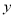
 ����
����