题目内容
如图，如果某个斜坡AB的长度为10米，且该斜坡最高点A到地面BC的铅垂高度为8米，求该斜坡的坡比
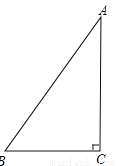
【解析】试题分析：首先根据AB和AC的长度以及勾股定理得出BC的长度，最后根据坡比的计算法则得出答案．
试题解析：∵某个斜坡AB的长度为10米，且该斜坡最高点A到地面BC的铅垂高度为8米，
∴水平距离BC= =6（m），
则该斜坡的坡比是： ．
某电子厂商投产一种新型电子产品，每件制造成本为18元，试销过程中发现，每月销售量y（万件）与销售单价x（元）之间的关系可以近似地看作一次函数y= -2x+100．（利润=售价-制造成本）
（1）写出每月的利润z（万元）与销售单价x（元）之间的函数关系式；
（2）当销售单价为多少元时，厂商每月能获得350万元的利润？当销售单价为多少元时，厂商每月能获得最大利润？最大利润是多少？
（1）z= -2x2+136x-1800；（2）当销售单价为34元时，每月能获得最大利润，最大利润是512万元；
【解析】试题分析：（1）根据每月的利润z=（x-18）y，再把y=-2x+100代入即可求出z与x之间的函数解析式，
（2）把z=350代入z=-2x2+136x-1800，解这个方程即可，将z═-2x2+136x-1800配方，得z=-2（x-34）2+512，即可求出当... 如图，已知抛物线y＝
x2－
x－3与x轴的交点为A、D(A在D的右侧)，与y轴的交点为C.
(1)直接写出A、D、C三点的坐标；
(2)若点M在抛物线上，使得△MAD的面积与△CAD的面积相等，求点M的坐标；
(3)设点C关于抛物线对称轴的对称点为B，在抛物线上是否存在点P，使得以A、B、C、P四点为顶点的四边形为梯形？若存在，请求出点P的坐标；若不存在，请说明理由．
（1）A点坐标为(4，0)，D点坐标为(－2，0)，C点坐标为(0，－3)；
（2）M点坐标为(2，－3)或(1＋，3)或(1－，3)；
（3）在抛物线上存在一点P，使得以点A、B、C、P四点为顶点所构成的四边形为梯形；点P的坐标为(－2，0)或(6，6)．
【解析】试题分析：（1）在中令，解得，
∴A(4，0) 、D(－2，0).
在中令，得，∴C(0，－3).
... 如图，正方形ABCD的边长为4cm，动点P、Q同时从点A出发，以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动，设运动时间为x(单位：s)，四边形PBDQ的面积为y(单位：cm2)，则y与x(0≤x≤8)之间的函数关系可以用图象表示为( )
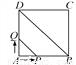
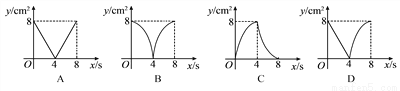
A. （A） B. （B） C. （C） D. （D）
B
【解析】试题分析：根据题意结合图形，分情况讨论：
①0≤x≤4时，根据四边形PBDQ的面积=△ABD的面积﹣△APQ的面积，列出函数关系式，从而得到函数图象；
②4≤x≤8时，根据四边形PBDQ的面积=△BCD的面积﹣△CPQ的面积，列出函数关系式，从而得到函数图象，再结合四个选项即可得解．
【解析】
①0≤x≤4时，
∵正方形的边长为4cm，
∴y=S△... 抛物线y＝x2＋bx＋c的图象先向右平移2个单位，再向下平移3个单位，所得图象的函数解析式为y＝(x－1)2－4，则b，c的值分别为( )
A. b＝2，c＝－6 B. b＝2，c＝0
C. b＝－6，c＝8 D. b＝－6，c＝2
B
【解析】试题分析：先确定出平移后的抛物线的顶点坐标，然后根据向右平移横坐标加，向下平移纵坐标减求出平移前的抛物线的顶点坐标，然后写出平移前的抛物线的顶点式形式，然后整理成一般形式，即可得到b、c的值．
【解析】
函数y=（x﹣1）2﹣4的顶点坐标为（1，﹣4），
∵是向右平移2个单位，再向下平移3个单位得到，
∴1﹣2=﹣1，﹣4+3=﹣1，
∴平移前的抛物线的... 河堤横断面如图所示，堤高BC=6米，迎水坡AB的坡比为1：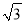 
则AB的长为_______
12米
【解析】试题分析：根据BC=6m，坡比为1： 可得：AC=6m，最后根据Rt△ABC的勾股定理可得：AB=12米． 如图，在坡角为30°的斜坡上要栽两棵树，要求它们之间的水平距离AC为6m，则这两棵树之间的坡面AB的长为（ ）
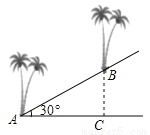
A. 12m B. 3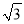
m C. 4
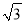m D. 12
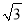m
C
【解析】试题分析：在Rt△ABC中，cos∠A=cos30°=，则AB=m，故选C． 抛物线y=x2－2x+3的顶点坐标是_______．
(1，2)
【解析】试题解析：∵y=x2-2x+3=x2-2x+1-1+3=（x-1）2+2，
∴抛物线y=x2-2x+3的顶点坐标是（1，2） 已知不论x为何值，x2-kx-15=(x+5)(x-3)，则k值为（ ）
A. 2 B. -2 C. 5 D. -3
B
【解析】∵x2-kx-15=(x+5)(x-3)=x2+2x-15，
∴k=-2.
故选B.