题目内容
4.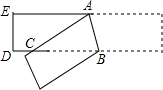 如图,将一张宽为2cm的长方形纸条折叠,折痕为AB,重叠部分为△ABC.如果∠ACB=30°,那么△ABC的面积等于4cm2.
如图,将一张宽为2cm的长方形纸条折叠,折痕为AB,重叠部分为△ABC.如果∠ACB=30°,那么△ABC的面积等于4cm2.
分析 根据折叠的性质得到∠1=∠BAC,而∠1=∠2,则∠2=∠BAC,从而可得到AC=BC,过A作AD⊥BC于D,则AD=2cm,而∠ABC=30°,根据含30°的直角三角形三边的关系得到AB=2AD=4cm,再利用三角形的面积公式计算即可.
解答 解:如图所示,过A作AD⊥BC于D.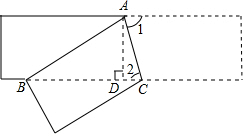
∵纸条为长方形,
∴∠1=∠2,
又∵长方形纸条折叠,折痕为AC,重叠部分为△ABC,
∴∠1=∠BAC,
∴∠2=∠BAC,
∴AC=BC
∵∠ABC=30°,
∴AB=2AD=4cm,
∴BC=AB=4cm,
∴△ABC的面积=$\frac{1}{2}$AD•BC=$\frac{1}{2}$×4×2=4(cm2).
故答案为:4cm2.
点评 本题考查了折叠的性质:折叠前后两图形全等,即对应线段相等,对应角相等.也考查了等腰三角形的判定定理以及含30°的直角三角形三边的关系.

练习册系列答案
相关题目
15.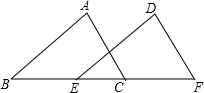 如图,B,C,E,F四点在一条直线上,下列条件能判定△ABC与△DEF全等的是( )
如图,B,C,E,F四点在一条直线上,下列条件能判定△ABC与△DEF全等的是( )
 如图,B,C,E,F四点在一条直线上,下列条件能判定△ABC与△DEF全等的是( )
如图,B,C,E,F四点在一条直线上,下列条件能判定△ABC与△DEF全等的是( )| A. | AB∥DE,∠A=∠D,BE=CF | B. | AB∥DE,AB=DE,AC=DF | ||
| C. | AB∥DE,AC=DF,BE=CF | D. | AB∥DE,AC∥DF,∠A=∠D |
14. 如图,AD是正五边形ABCDE的一条对角线,则∠BAD等于( )
如图,AD是正五边形ABCDE的一条对角线,则∠BAD等于( )
 如图,AD是正五边形ABCDE的一条对角线,则∠BAD等于( )
如图,AD是正五边形ABCDE的一条对角线,则∠BAD等于( )| A. | 72° | B. | 108° | C. | 36° | D. | 62° |
 由一个英文单词由五个字母组成,分别对应如图中的有序数对,顺次为(5,3),(6,3),(7,3),(4,1),(4,4),请你把这个英文单词写出来并翻译成中文为study,“学习”.
由一个英文单词由五个字母组成,分别对应如图中的有序数对,顺次为(5,3),(6,3),(7,3),(4,1),(4,4),请你把这个英文单词写出来并翻译成中文为study,“学习”.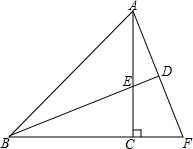 如图,已知等腰直角三角形ABC中,CA=CB,BE平分∠ABC且交AC边于点E,点F在BC的延长线上,∠CAF=∠CBE,延长BE交AF于点D.
如图,已知等腰直角三角形ABC中,CA=CB,BE平分∠ABC且交AC边于点E,点F在BC的延长线上,∠CAF=∠CBE,延长BE交AF于点D.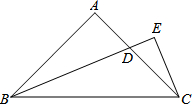 等腰直角三角形ABC中,∠A=90°,∠B的平分线交AC于D,过点C向BD作垂线,并与BD延长线交于点E,求证:BD=2CE.
等腰直角三角形ABC中,∠A=90°,∠B的平分线交AC于D,过点C向BD作垂线,并与BD延长线交于点E,求证:BD=2CE.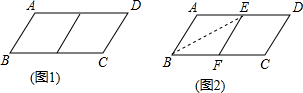
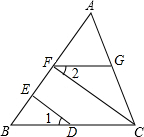 如图,∠1=∠2,CF⊥AB,DE⊥AB,求证:FG∥BC.
如图,∠1=∠2,CF⊥AB,DE⊥AB,求证:FG∥BC.