题目内容
9.(1)计算:$-{2^{-2}}+|{1-\frac{1}{{sin{{45}°}}}}|•({\sqrt{8}+2})$(2)先化简,再求代数式的值:$({\frac{2}{a+1}+\frac{a+2}{{{a^2}-1}}})÷\frac{a}{a+1}$,其中a=(-1)2014+tan60°.
分析 (1)分别根据负整数指数幂的计算法则、特殊角的三角函数值及绝对值的性质分别计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先根据实数混合运算的法则把原式进行化简,再求出a的值代入进行计算即可.
解答 (1)解:原式=-$\frac{1}{4}$+|1-$\frac{1}{\sqrt{2}}$|•(2+2$\sqrt{2}$)
=-$\frac{1}{4}$+|1-$\sqrt{2}$|×2(1+$\sqrt{2}$)
=-$\frac{1}{4}$+2($\sqrt{2}$-1)($\sqrt{2}$+1)
=-$\frac{1}{4}$+2
=$\frac{7}{4}$;
(2)原式=$\frac{2a-2+a+2}{(a+1)(a-1)}$•$\frac{a+1}{a}$=$\frac{3}{a-1}$,
∵a=1+$\sqrt{3}$,
∴原式=$\frac{3}{\sqrt{3}}$=$\sqrt{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
19.若$\frac{x+y}{y}=\frac{7}{4}$,那么$\frac{y}{x}$的值是( )
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
17.凤水小区2013年屋顶绿化面积为3 000平方米,计划2015年屋顶绿化面积要达到4 320平方米.如果每年屋顶绿化面积的增长率都为x,那么x满足的方程是( )
| A. | 3 000(1+x)=4 320 | B. | 3 000(1+x)2=4 320 | ||
| C. | 3 000(1-x%)2=4 320 | D. | 3 000x2=4 320 |
4.下列各数中,倒数是-3的数是( )
| A. | 3 | B. | -3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
14.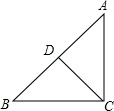 如图,在△ABC中,点D在AB上,下列条件能使△BCD和△ABC相似的是( )
如图,在△ABC中,点D在AB上,下列条件能使△BCD和△ABC相似的是( )
 如图,在△ABC中,点D在AB上,下列条件能使△BCD和△ABC相似的是( )
如图,在△ABC中,点D在AB上,下列条件能使△BCD和△ABC相似的是( )| A. | ∠ACD=∠B | B. | ∠ADC=∠ACB | C. | AC2=AD•AB | D. | BC2=BD•BA |
19.已知反比例函数图象经过点(1,-1),(m,1),则m等于( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
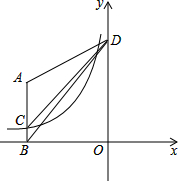 如图,点D为y轴上任意一点,过点A(-6,4)作AB垂直于x轴于点B,AB交反比例函数y=-$\frac{6}{x}$(x<0)于点C,则△ADC的面积为9.
如图,点D为y轴上任意一点,过点A(-6,4)作AB垂直于x轴于点B,AB交反比例函数y=-$\frac{6}{x}$(x<0)于点C,则△ADC的面积为9.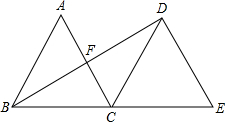 如图,△ABC是边长为2的等边三角形,将△ABC沿直线BC平移到△DCE的位置,连接BD,求△ABC平移的距离和BD的长.
如图,△ABC是边长为2的等边三角形,将△ABC沿直线BC平移到△DCE的位置,连接BD,求△ABC平移的距离和BD的长.