题目内容
1.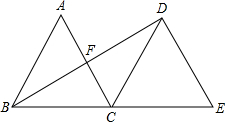 如图,△ABC是边长为2的等边三角形,将△ABC沿直线BC平移到△DCE的位置,连接BD,求△ABC平移的距离和BD的长.
如图,△ABC是边长为2的等边三角形,将△ABC沿直线BC平移到△DCE的位置,连接BD,求△ABC平移的距离和BD的长.
分析 由平移的性质可知△ABC平移的距离,以及BE=2BC=4,DE=AC=2,故可得出BD⊥DE,由∠E=∠ACB=60°,在Rt△BDE中利用勾股定理即可得出BD的长.
解答 解:∵△DCE由△ABC平移而成,
∴△ABC平移的距离为:BC=2,
且BE=2BC=4,DE=AC=2,∠E=∠ACB=60°,
∴DE=$\frac{1}{2}$BE,
∴BD⊥DE,
又∵∠E=∠ACB=60°,
∴AC∥DE,
∴BD⊥AC,
∴△BED是直角三角形,
∵BE=4,DE=2,
∴BD=$\sqrt{B{E}^{2}-D{E}^{2}}$=2$\sqrt{3}$.
点评 本题考查的是等边三角形的性质及平移的性质,熟知图形平移后的图形与原图形全等的性质是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.下列运算正确的是( )
| A. | (a-b)2=a2-b2 | B. | 3a2-2a2=a2 | C. | -2(a-1)=-2a-1 | D. | a6÷a3=a2 |
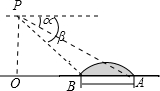 如图,直升飞机在跨河大桥AB的上方P点处,此时飞机离地面的高度PO=450m,且A、B、O三点在一条直线上,测得大桥两端的俯角分别为∠α=28°,∠β=43°,求大桥AB的长.(精确到1m)
如图,直升飞机在跨河大桥AB的上方P点处,此时飞机离地面的高度PO=450m,且A、B、O三点在一条直线上,测得大桥两端的俯角分别为∠α=28°,∠β=43°,求大桥AB的长.(精确到1m)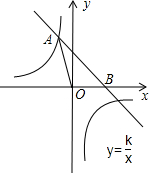 如图,已知直线y=-x+4与反比例函数的图象相交于点A(-2,a),并且与x轴相交于点B.
如图,已知直线y=-x+4与反比例函数的图象相交于点A(-2,a),并且与x轴相交于点B. 在△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是AB的中点,求∠ECD的度数.
在△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是AB的中点,求∠ECD的度数.