题目内容
14．
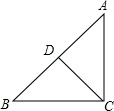如图，在△ABC中，点D在AB上，下列条件能使△BCD和△ABC相似的是（ ）| A． | ∠ACD=∠B | B． | ∠ADC=∠ACB | C． | AC2=AD•AB | D． | BC2=BD•BA |
分析 由两边对应成比例且夹角相等得到三角形相似即可得证．
解答 解：若BC2=BD•BA，则有$\frac{BC}{BA}$=$\frac{BD}{BC}$，且∠B=∠B，
∴△BCD∽△BAC，
故选D
点评 此题考查了相似三角形的判定，熟练掌握相似三角形的判定方法是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
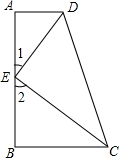如图所示，AD⊥AB，DE，CE分别是∠ADC与∠BCD的平分线，∠1+∠2=90°，AD与BC平行吗？为什么？
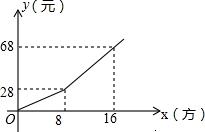为鼓励市民节约用水，某市自来水公司按分段收费标准收费，如图反映的是每月所收水费y（元）与用水量x（方）之间的函数关系．
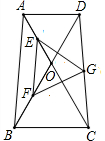在梯形ABCD中，AD∥BC，AB=CD，∠AOD=60°，E为OA的中点，F为OB的中点，G为CD的中点，试判断△EFG的形状并说明理由．
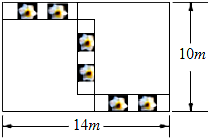某市举办花展，如图，在长为14m，宽为10m的长方形展厅，划出三个形状、大小完全一样的小长方形摆放水仙花，则每个小长方形的周长为（ ）
如图，AB是圆O的直径，弦CD⊥AB于点E，点P在圆O上且∠1=∠C．