题目内容
17.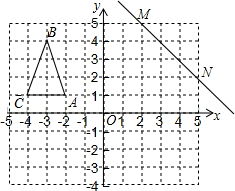 如图,在直角坐标系中有一个格点三角形ABC(顶点都在格点上的三角形),已知A(-2,1),B(-3,4),C(-4,1),直线MN过点M(2,5),N(5,2).
如图,在直角坐标系中有一个格点三角形ABC(顶点都在格点上的三角形),已知A(-2,1),B(-3,4),C(-4,1),直线MN过点M(2,5),N(5,2).(1)请在图中作出格点三角形ABC关于x轴对称的格点三角形A′B′C′(A,B,C的对应点依次为A′,B′,C′);
(2)连结AM,AN,则tan∠MAN=$\frac{3}{4}$.
分析 (1)根据关于x轴对称的点的坐标特点可得A′,B′,C′的坐标,再顺次连接即可;
(2)根据网格图可得:∠AMN=90°,利用勾股定理可计算出MN、AM的长,再根据正切定义可得答案.
解答 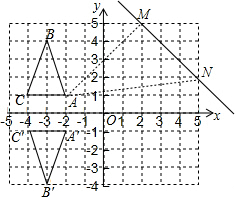 解:(1)如图所示:
解:(1)如图所示:
(2)由网格图可得:∠AMN=90°,
∵MN=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,AM=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$,
∴tan∠MAN=$\frac{NM}{AM}$=$\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 此题主要考查了作图--轴对称变换,以及三角函数,关键是掌握正切=$\frac{对边}{邻边}$.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
12.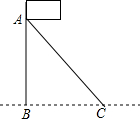 如图,AC是旗杆AB的一根拉线,测得BC=6米,∠ACB=50°,则拉线AC的长为( )
如图,AC是旗杆AB的一根拉线,测得BC=6米,∠ACB=50°,则拉线AC的长为( )
 如图,AC是旗杆AB的一根拉线,测得BC=6米,∠ACB=50°,则拉线AC的长为( )
如图,AC是旗杆AB的一根拉线,测得BC=6米,∠ACB=50°,则拉线AC的长为( )| A. | 6sin50° | B. | 6cos50° | C. | $\frac{6}{sin50°}$ | D. | $\frac{6}{cos50°}$ |
9.下列计算正确的是( )
| A. | 2a5+a5=3a10 | B. | a2•a3=a6 | C. | (a2)3=a5 | D. | a10÷a2=a8 |
 已知实数a,b在数轴上的对应点如图所示,化简:$\sqrt{(a-b)^{2}}$-$\sqrt{{a}^{2}}$.
已知实数a,b在数轴上的对应点如图所示,化简:$\sqrt{(a-b)^{2}}$-$\sqrt{{a}^{2}}$.