题目内容
12.△ABC是等边三角形,以点C为旋转中心,将线段CA按顺时针方向旋转60°得到线段CD,连接BD交AC于点O.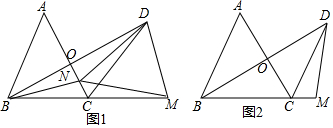
(1)如图1.
①求证:AC垂直平分BD;
①点M在BC的延长线上,点N在线段CO上,且ND=NM,连接BN,判断△MND的形状,并加以证明;
(2)如图2,点M在BC的延长线上,点N在线段AO上,且ND=NM,补全图2,求证:NA=MC.
分析 (1)根据等边三角形的性质和旋转的性质证明即可;
(2)根据等边三角形的性质和全等三角形的判定方法,证明△AND≌△CMD,再利用全等三角形的对应边相等证明即可.
解答 证明:∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠CAB=60°,
①以点C为旋转中心,将线段CA按顺时针方向旋转60°得到线段CD,
∴CD=CA,∠ACD=∠ACB=60°,
∴BO=DO,CO⊥BD,
∴AC垂直平分BD;
②△MND是等边三角形,
如图1,由①知AC垂直平分BD,
∴NB=ND,∠CBD=$\frac{1}{2}$∠ABC=30°,
∴∠1=∠2,
∴∠BND=180°-2∠2,
∵ND=NM,
∴NB=NM,
∴∠3=∠4,∠BNM=180°-2∠4,
∴∠DNM=360°-180°+2∠2-180°+2∠4=2(∠2+∠4)=60°,
∴△MND是等边三角形;
(2)连接AD,BN,如图2,
由题意知,△ACD是等边三角形,
∴∠ADC=60°,AD=CD,
与(1)同理可证∠1=∠2,∠3=∠NBM,
∠BND=180°-2∠2,∠BNM=180°-2∠NBM,
∴∠MND=∠BND-∠BNM=2(∠NBM-∠2)=60°,
∵ND=NM,
∴△MND是等边三角形,
∴DN=DM,∠NDM=60°,∠ADC=∠NDM,
∴∠NDA=∠MDC,
在△AND与△MDC中
$\left\{\begin{array}{l}{DN=DM}\\{∠NDA=∠NDM}\\{AD=DC}\end{array}\right.$,
∴△AND≌△CMD,
∴NA=MC.
点评 本题主要考查线段的旋转、全等三角形的性质和判定、等边三角形的性质等,解决此题的关键是能将三角形的判定和性质、等边三角形的相关性质灵活的应用.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
2.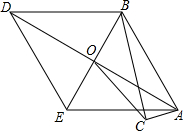 如图,在△ABC中,∠ACB=90°,AC=1,BC=2$\sqrt{3}$,以AB为边向左作菱形ABDE,使∠BAE=60°,AD,BE相交于点O,则CO的长是( )
如图,在△ABC中,∠ACB=90°,AC=1,BC=2$\sqrt{3}$,以AB为边向左作菱形ABDE,使∠BAE=60°,AD,BE相交于点O,则CO的长是( )
 如图,在△ABC中,∠ACB=90°,AC=1,BC=2$\sqrt{3}$,以AB为边向左作菱形ABDE,使∠BAE=60°,AD,BE相交于点O,则CO的长是( )
如图,在△ABC中,∠ACB=90°,AC=1,BC=2$\sqrt{3}$,以AB为边向左作菱形ABDE,使∠BAE=60°,AD,BE相交于点O,则CO的长是( )| A. | $\frac{5}{2}$ | B. | 3 | C. | $\frac{9}{4}$ | D. | $\sqrt{6}$ |
3.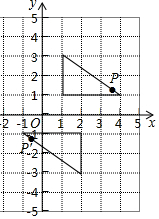 两个完全相同的三角形纸片,在平面直角坐标系中的摆放位置如图所示,点P与点P′是一对对应点,若点P的坐标为(a,b),则点P′的坐标为( )
两个完全相同的三角形纸片,在平面直角坐标系中的摆放位置如图所示,点P与点P′是一对对应点,若点P的坐标为(a,b),则点P′的坐标为( )
 两个完全相同的三角形纸片,在平面直角坐标系中的摆放位置如图所示,点P与点P′是一对对应点,若点P的坐标为(a,b),则点P′的坐标为( )
两个完全相同的三角形纸片,在平面直角坐标系中的摆放位置如图所示,点P与点P′是一对对应点,若点P的坐标为(a,b),则点P′的坐标为( )| A. | (b+3,a) | B. | (b,3-a) | C. | (a-3,-b) | D. | (3-a,-b) |
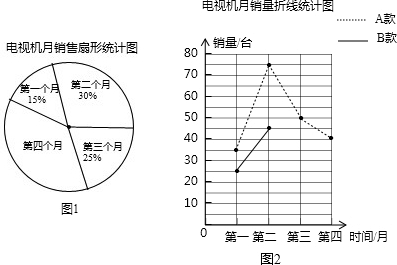

 如图,由直径分别为4厘米、6厘米和10厘米的三个半圆所组成的图形,则图中阴影部分的面积为10π 平方厘米.
如图,由直径分别为4厘米、6厘米和10厘米的三个半圆所组成的图形,则图中阴影部分的面积为10π 平方厘米.