题目内容
 已知二次函数y=x2+bx+c,其图象抛物线交x轴于点A(1,0),B(3,0),交y轴于点C,直线l过点C,且交抛物线于另一点E(点E不与点A、B重合).
已知二次函数y=x2+bx+c,其图象抛物线交x轴于点A(1,0),B(3,0),交y轴于点C,直线l过点C,且交抛物线于另一点E(点E不与点A、B重合).(1)求此二次函数关系式;
(2)若直线l1经过抛物线顶点D,交x轴于点F,且l1∥l,则以点C、D、E、F为顶点的四边形能否为平行四边形?若能,求出点E的坐标;若不能,请说明理由.
(3)若过点A作AG⊥x轴,交直线l于点G,连接OG、BE,试证明OG∥BE.
考点:二次函数综合题
专题:代数几何综合题,压轴题
分析:(1)由二次函数y=x2+bx+c,其图象抛物线交x轴于点A(1,0),B(3,0),直接利用待定系数法求解,即可求得此二次函数关系式;
(2)以点C、D、E、F为顶点的四边形构成平行四边形,有两种情形,需要分类讨论,避免漏解:
①若CD为平行四边形的对角线,如答图2-1所示;
②若CD为平行四边形的边,如答图2-2所示;
(3)首先过点E作EH⊥x轴于点H,设直线CE的解析式为:y=kx+3,然后分别求得点G与E的坐标,即可证得△OAG∽△BHE,则可得∠AOG=∠HBE,继而可证得OG∥BE.
(2)以点C、D、E、F为顶点的四边形构成平行四边形,有两种情形,需要分类讨论,避免漏解:
①若CD为平行四边形的对角线,如答图2-1所示;
②若CD为平行四边形的边,如答图2-2所示;
(3)首先过点E作EH⊥x轴于点H,设直线CE的解析式为:y=kx+3,然后分别求得点G与E的坐标,即可证得△OAG∽△BHE,则可得∠AOG=∠HBE,继而可证得OG∥BE.
解答:解:(1)二次函数y=x2+bx+c,其图象抛物线交x轴于点A(1,0),B(3,0),
∴
,
解得:
,
∴此二次函数关系式为:y=x2-4x+3;
(2)假设以点C、D、E、F为顶点的四边形能成为平行四边形.
①若CD为平行四边形的对角线,如答图2-1.
过点D作DM⊥AB于点M,过点E作EN⊥OC于点N,
∵y=x2-4x+3=(x-2)2-1,
∴点D(2,-1),点C(0,3),
∴DM=1,
∵l1∥l,
∴当CE=DF时,四边形CEDF是平行四边形,
∴∠ECF+∠CFD=180°,
∵∠OCF+∠OFC=90°,
∴∠ECN+∠DFM=90°,
∵∠DFM+∠FDM=90°,
∴∠ECN=∠FDM,
在△ECN和△FDM中,
,
∴△ECN≌△FDM(AAS),
∴CN=DM=1,
∴ON=OC-CN=3-1=2,
当y=2时,x2-4x+3=2,
解得:x=2±
;
当x=2±
时,可得E(2+
,2),F(-
,0)或E(2-
,2,),F(
,0),
此时四边形CFDE为平行四边形.

②若CD为平行四边形的边,如答图2-2,则EF∥CD,且EF=CD.
过点D作DM⊥y轴于点M,则DM=2,OM=1,CM=OM+OC=4;
过点E作EN⊥x轴于点N.
易证△CDM≌△EFN,∴EN=CM=4.
∴x2-4x+3=4,
解得:x=2±
.
综上所述,以点C、D、E、F为顶点的四边形能成为平行四边形;点E的坐标为(2+
,2)、(2-
,2)、(2+
,4)、(2-
,4).
 (3)如图②,过点E作EH⊥x轴于点H,
(3)如图②,过点E作EH⊥x轴于点H,
设直线CE的解析式为:y=kx+3,
∵A(1,0),AG⊥x轴,
∴点G(1,k+3),
即OA=1,AG=k+3,
∵E是直线与抛物线的交点,
∴
,
解得:
,
∴点E(k+4,(k+1)(k+3)),
∴BH=OH-OB=k+1,EH=(k+1)(k+3),
∴
=
=
,
∵∠OAG=∠BHE=90°,
∴△OAG∽△BHE,
∴∠AOG=∠HBE,
∴OG∥BE.
∴
|
解得:
|
∴此二次函数关系式为:y=x2-4x+3;
(2)假设以点C、D、E、F为顶点的四边形能成为平行四边形.
①若CD为平行四边形的对角线,如答图2-1.
过点D作DM⊥AB于点M,过点E作EN⊥OC于点N,
∵y=x2-4x+3=(x-2)2-1,
∴点D(2,-1),点C(0,3),
∴DM=1,
∵l1∥l,
∴当CE=DF时,四边形CEDF是平行四边形,
∴∠ECF+∠CFD=180°,
∵∠OCF+∠OFC=90°,
∴∠ECN+∠DFM=90°,
∵∠DFM+∠FDM=90°,
∴∠ECN=∠FDM,
在△ECN和△FDM中,
|
∴△ECN≌△FDM(AAS),
∴CN=DM=1,
∴ON=OC-CN=3-1=2,
当y=2时,x2-4x+3=2,
解得:x=2±
| 3 |
当x=2±
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
此时四边形CFDE为平行四边形.

②若CD为平行四边形的边,如答图2-2,则EF∥CD,且EF=CD.
过点D作DM⊥y轴于点M,则DM=2,OM=1,CM=OM+OC=4;
过点E作EN⊥x轴于点N.
易证△CDM≌△EFN,∴EN=CM=4.
∴x2-4x+3=4,
解得:x=2±
| 5 |
综上所述,以点C、D、E、F为顶点的四边形能成为平行四边形;点E的坐标为(2+
| 3 |
| 3 |
| 5 |
| 5 |
 (3)如图②,过点E作EH⊥x轴于点H,
(3)如图②,过点E作EH⊥x轴于点H,设直线CE的解析式为:y=kx+3,
∵A(1,0),AG⊥x轴,
∴点G(1,k+3),
即OA=1,AG=k+3,
∵E是直线与抛物线的交点,
∴
|
解得:
|
∴点E(k+4,(k+1)(k+3)),
∴BH=OH-OB=k+1,EH=(k+1)(k+3),
∴
| OA |
| BH |
| AG |
| EH |
| 1 |
| k+1 |
∵∠OAG=∠BHE=90°,
∴△OAG∽△BHE,
∴∠AOG=∠HBE,
∴OG∥BE.
点评:此题属于二次函数的综合题、综合性较强,难度较大,主要考查了待定系数法求二次函数的解析式、一次函数与二次函数的交点问题、平行四边形的性质以及相似三角形的判定与性质等知识.注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目


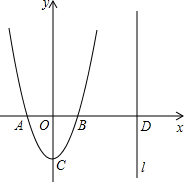 如图,二次函数y=ax2+c的图象交x轴于A、B两点,点A坐标为(-1,0),顶点C的坐标为(0,-2),点D在x轴上,过点D作直线l垂直于x轴,设点D的横坐标为m(m>1).
如图,二次函数y=ax2+c的图象交x轴于A、B两点,点A坐标为(-1,0),顶点C的坐标为(0,-2),点D在x轴上,过点D作直线l垂直于x轴,设点D的横坐标为m(m>1).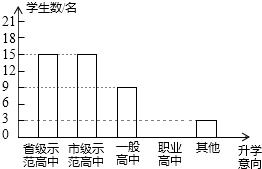 近几年我市加大中职教育投入力度,取得了良好的社会效果.某校随机调查了九年级m名学生的升学意向,并根据调查结果绘制出如下不完整的统计图表:
近几年我市加大中职教育投入力度,取得了良好的社会效果.某校随机调查了九年级m名学生的升学意向,并根据调查结果绘制出如下不完整的统计图表: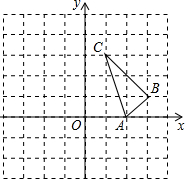 如图在平面直角坐标系中,△ABC的顶点坐标分别为A(2,0),B(3,1),C(1,3);
如图在平面直角坐标系中,△ABC的顶点坐标分别为A(2,0),B(3,1),C(1,3);
 甲、乙、丙三人进行飞镖比赛,已知他们每人五次投得的成绩如图,那么三人中成绩最稳定的是
甲、乙、丙三人进行飞镖比赛,已知他们每人五次投得的成绩如图,那么三人中成绩最稳定的是