题目内容
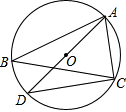 如图所示,已知⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD.若AD=5,AC=4,则cosB的值为( )
如图所示,已知⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD.若AD=5,AC=4,则cosB的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:圆周角定理,勾股定理,锐角三角函数的定义
专题:计算题
分析:根据圆周角定理由AD是⊙O的直径得∠ACD=90°,在Rt△ACD中,利用勾股定理计算出CD=3,则根据余弦的定义得cosD=
,然后根据圆周角定理得∠B=∠D,所以cosB=
.
| 3 |
| 5 |
| 3 |
| 5 |
解答:解:∵AD是⊙O的直径,
∴∠ACD=90°,
在Rt△ACD中,AD=5,AC=4,
∴CD=
=3,
∴cosD=
=
,
∵∠B=∠D,
∴cosB=
.
故选D.
∴∠ACD=90°,
在Rt△ACD中,AD=5,AC=4,
∴CD=
| AD2-AC2 |
∴cosD=
| CD |
| AD |
| 3 |
| 5 |
∵∠B=∠D,
∴cosB=
| 3 |
| 5 |
故选D.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了勾股定理和锐角三角函数的定义.

练习册系列答案
相关题目
要组织一次排球邀请赛,参赛的每两个各队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应邀请多少个队参赛?若设应邀请x个队参赛,可列出的方程为( )
| A、x(x+1)=28 | ||
| B、x(x-1)=28 | ||
C、
| ||
D、
|
 如图,在△ABC中,∠BAC=30°,AB=AC,AD是BC边上的中线,∠ACE=
如图,在△ABC中,∠BAC=30°,AB=AC,AD是BC边上的中线,∠ACE=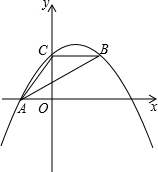 如图,抛物线y=ax2+bx+c经过A(-3,0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.
如图,抛物线y=ax2+bx+c经过A(-3,0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.
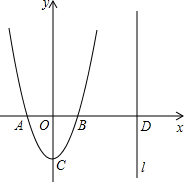 如图,二次函数y=ax2+c的图象交x轴于A、B两点,点A坐标为(-1,0),顶点C的坐标为(0,-2),点D在x轴上,过点D作直线l垂直于x轴,设点D的横坐标为m(m>1).
如图,二次函数y=ax2+c的图象交x轴于A、B两点,点A坐标为(-1,0),顶点C的坐标为(0,-2),点D在x轴上,过点D作直线l垂直于x轴,设点D的横坐标为m(m>1).