题目内容
设二次函数f(x)=ax2+bx+c(a<0),方程f(x)=x的根为x1、x2,且x2-x1>
,当0<t<x1时,试比较f(t)与x1的大小关系.
| 1 |
| a |
考点:抛物线与x轴的交点
专题:
分析:方程f(t)-x=0的两个根x1,x2,所以构造函数,当0<t<x1时,利用函数的性质推出x<f (t),然后作差x1-f(t),化简分析出f(t)<x1,即可.
解答:解:令F(x)=f(t)-x.因为x1,x2是方程f(t)-x=0的根,所以
F(t)=a(x-x1)(x-x2).
当0<t<x1时,由于x1<x2,得(x-x1)(x-x2)>0,又a<0,得
F(t)=a(x-x1)(x-x2)>0,
即x<f(t).
x1-f(t)
=x1-[x+F(t)]
=x1-x+a(x1-x)(x-x2)
=(x1-x)[1+a(x-x2)]
因为x2-x1>
,所以x1-x>0,1+a(x-x2)=1+ax-ax2>1-ax2>0.
得x1-f(t)>0.
由此得f(t)<x1.
F(t)=a(x-x1)(x-x2).
当0<t<x1时,由于x1<x2,得(x-x1)(x-x2)>0,又a<0,得
F(t)=a(x-x1)(x-x2)>0,
即x<f(t).
x1-f(t)
=x1-[x+F(t)]
=x1-x+a(x1-x)(x-x2)
=(x1-x)[1+a(x-x2)]
因为x2-x1>
| 1 |
| a |
得x1-f(t)>0.
由此得f(t)<x1.
点评:本小题主要考查一元二次方程、二次函数和不等式的基础知识,考查综合运用数学知识分析问题和解决问题的能力.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
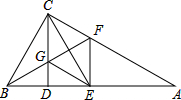 如图,在△ABC中,∠ACB=90°,BF平分∠ABC,CD⊥AB于点D,与BF交于点G,GE∥AC.求证:CE与FG互相垂直平分.
如图,在△ABC中,∠ACB=90°,BF平分∠ABC,CD⊥AB于点D,与BF交于点G,GE∥AC.求证:CE与FG互相垂直平分. 如图,在△ABC中,∠ABC的平分线交AC于点D,DE∥BC.求证:△EBD是等腰三角形.
如图,在△ABC中,∠ABC的平分线交AC于点D,DE∥BC.求证:△EBD是等腰三角形. 如图,有A,B,C三个村庄,他们合作打一口井,为了公平,需要这口井到三个村庄的距离相等,那么,这口井应该在哪个位置?请画出来.
如图,有A,B,C三个村庄,他们合作打一口井,为了公平,需要这口井到三个村庄的距离相等,那么,这口井应该在哪个位置?请画出来.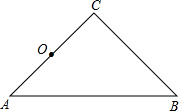 如图,在等腰△ABC中,∠C=90°,AB=4
如图,在等腰△ABC中,∠C=90°,AB=4