题目内容
16.分解因式:(1)15a2-5a
(2)(a2+1)2-4a2
(3)x2-2xy+y2-1
(4)4a3b2-12a2b2+8ab2.
分析 (1)原式提取公因式即可;
(2)原式利用平方差公式化简,再利用完全平方公式分解即可;
(3)原式前三项利用完全平方公式分解,再利用平方差公式分解即可;
(4)原式提取公因式,再利用十字相乘法分解即可.
解答 解:(1)原式=5a(3a-1);
(2)原式=(a2+1+2a)(a2+1-2a)=(a+1)2(a-1)2;
(3)原式=(x-y)2-1=(x-y+1)(x-y-1);
(4)原式=4ab2(a2-3a+2)=4ab2(a-1)(a-2).
点评 此题考查了因式分解-运用公式法,以及提公因式法,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
相关题目
11.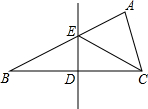 如图,在△ABC中,BA=BC,∠B=30°,BC的垂直平分线交AB于E,垂足为D,若ED=1,则EC的长为( )
如图,在△ABC中,BA=BC,∠B=30°,BC的垂直平分线交AB于E,垂足为D,若ED=1,则EC的长为( )
 如图,在△ABC中,BA=BC,∠B=30°,BC的垂直平分线交AB于E,垂足为D,若ED=1,则EC的长为( )
如图,在△ABC中,BA=BC,∠B=30°,BC的垂直平分线交AB于E,垂足为D,若ED=1,则EC的长为( )| A. | 1 | B. | 1+$\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
6.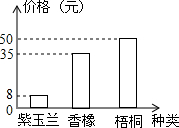 为了响应市政府提出的“创建森林城市”的号召,市林业局计划今年在瓯江口新区种植梧桐、紫玉兰和香樟三类树苗,其中香樟树苗的株数是梧桐树苗的2倍,三种树苗的单价如图所示,设计划种植x株梧桐树苗,y株紫玉兰树苗;
为了响应市政府提出的“创建森林城市”的号召,市林业局计划今年在瓯江口新区种植梧桐、紫玉兰和香樟三类树苗,其中香樟树苗的株数是梧桐树苗的2倍,三种树苗的单价如图所示,设计划种植x株梧桐树苗,y株紫玉兰树苗;
(1)根据信息,完成表格:
(2)若三种树苗共种植150株,购买树苗共花费5040元,那么三种树苗分别种植了多少株?
(3)若购买树苗的总费用是7232元,那么最少能种植树苗64株.
 为了响应市政府提出的“创建森林城市”的号召,市林业局计划今年在瓯江口新区种植梧桐、紫玉兰和香樟三类树苗,其中香樟树苗的株数是梧桐树苗的2倍,三种树苗的单价如图所示,设计划种植x株梧桐树苗,y株紫玉兰树苗;
为了响应市政府提出的“创建森林城市”的号召,市林业局计划今年在瓯江口新区种植梧桐、紫玉兰和香樟三类树苗,其中香樟树苗的株数是梧桐树苗的2倍,三种树苗的单价如图所示,设计划种植x株梧桐树苗,y株紫玉兰树苗;(1)根据信息,完成表格:
| 梧桐 | 香樟 | 紫玉兰 | 合计 | |
| 树苗株数 | x | 2x | y | 3x+y |
| 费用 | 50x | 70x | 8y | 120x+8y |
(3)若购买树苗的总费用是7232元,那么最少能种植树苗64株.
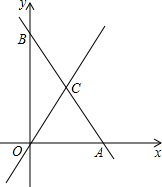 在平面直角坐标系中,直线AB的解析式为y=-2x+12,点C是线段AB的中点.
在平面直角坐标系中,直线AB的解析式为y=-2x+12,点C是线段AB的中点.