题目内容
1.(1)若a-b=2$\sqrt{3}$,ab=2,求a3b+ab3的值;(2)用简便简便方法计算:
$\frac{201{4}^{3}-2×201{4}^{2}-2012}{201{4}^{3}+201{4}^{2}-2015}$.
分析 (1)利用提取公因式法和完全平方公式整理,进一步整体代入求得答案即可;
(2)把分子分母逐步提取公因式分解因式约分得出答案即可.
解答 解:(1)∵a-b=2$\sqrt{3}$,ab=2,
∴a3b+ab3
=ab(a2+b2)
=ab[(a-b)2+2ab]
=2×(12+4)
=32.
(2)原式=$\frac{201{4}^{2}×(2014-2)-2012}{201{4}^{2}×(2014+1)-2015}$
=$\frac{2012×(201{4}^{2}-1)}{2015×(201{4}^{2}-1)}$
=$\frac{2012}{2015}$.
点评 此题考查因式分解的实际运用,掌握提取公因式法和完全平方公式是解决问题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
12. 如图,若AB是⊙O的直径,CD是⊙O的弦,∠BCD=35°,则∠ABD的度数为( )
如图,若AB是⊙O的直径,CD是⊙O的弦,∠BCD=35°,则∠ABD的度数为( )
 如图,若AB是⊙O的直径,CD是⊙O的弦,∠BCD=35°,则∠ABD的度数为( )
如图,若AB是⊙O的直径,CD是⊙O的弦,∠BCD=35°,则∠ABD的度数为( )| A. | 65° | B. | 35° | C. | 55° | D. | 60° |
9.三角形的内心是( )
| A. | 三边垂直平分线的交点 | B. | 三条角平分线的交点 | ||
| C. | 三条高所在直线的交点 | D. | 三条中线的交点 |
 如图所示,A、B两个旅游点从2011年至2015年“清明小长假”期间的旅游人数变化情况分别用实线和虚线表示,请解答以下问题:
如图所示,A、B两个旅游点从2011年至2015年“清明小长假”期间的旅游人数变化情况分别用实线和虚线表示,请解答以下问题: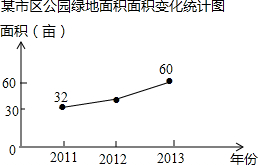 市区某公园的总面积为180亩,它的绿化给公园周边的环境带来了明显的改善,如图是该公园绿地面积的变化统计图,其中2013年绿地面积的增长率是2012年增长率的两倍.
市区某公园的总面积为180亩,它的绿化给公园周边的环境带来了明显的改善,如图是该公园绿地面积的变化统计图,其中2013年绿地面积的增长率是2012年增长率的两倍.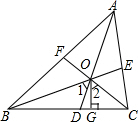 已知,如图,点O是△ABC的三条角平分线的交点,作OG⊥BC,垂足为点G,求证:∠1=∠2.
已知,如图,点O是△ABC的三条角平分线的交点,作OG⊥BC,垂足为点G,求证:∠1=∠2.