题目内容
已知二次函数y=ax2+bx+c的图象过(0,-6)、(1,0)和(-2,-6)三点.
(1)求二次函数解析式;
(2)求二次函数图象的顶点坐标;
(3)若点A(m-2n,-8mn-10)在此二次函数图象上,求m、n的值.
(1)求二次函数解析式;
(2)求二次函数图象的顶点坐标;
(3)若点A(m-2n,-8mn-10)在此二次函数图象上,求m、n的值.
考点:待定系数法求二次函数解析式,二次函数的性质,二次函数图象上点的坐标特征
专题:
分析:(1)将点(0,-6)、(1,0)和(-2,-6)代入二次函数的解析式y=ax2+bx+c,利用待定系数法求得这个二次函数的解析式;
(2)利用(1)的结果,将二次函数的解析式转化为顶点式,然后根据解析式求这个二次函数的顶点坐标;
(3)将点A(m-2n,-8mn-10)代入y=2x2+4x-6,整理后得(m+1)2+(2n-1)2=0,即可得m=-1,n=
.
(2)利用(1)的结果,将二次函数的解析式转化为顶点式,然后根据解析式求这个二次函数的顶点坐标;
(3)将点A(m-2n,-8mn-10)代入y=2x2+4x-6,整理后得(m+1)2+(2n-1)2=0,即可得m=-1,n=
| 1 |
| 2 |
解答:解:(1)由已知得
,解得
,
∴二次函数解析式为:y=2x2+4x-6;
(2)∵y=2x2+4x-6=2(x+1)2-8,
∴顶点坐标为(-1,-8);
(3)由已知,得-8mn-10=2(m-2n)2+4(m-2n)-6
m2+4n2+2m-4n+2=0
(m+1)2+(2n-1)2=0
∴m=-1,n=
.
|
|
∴二次函数解析式为:y=2x2+4x-6;
(2)∵y=2x2+4x-6=2(x+1)2-8,
∴顶点坐标为(-1,-8);
(3)由已知,得-8mn-10=2(m-2n)2+4(m-2n)-6
m2+4n2+2m-4n+2=0
(m+1)2+(2n-1)2=0
∴m=-1,n=
| 1 |
| 2 |
点评:本题考查了待定系数法求二次函数的解析式、二次函数的三种形式.将二次函数的一般解析式转化为顶点式时,可采用了“配方法”.

练习册系列答案
相关题目

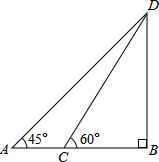 某校数学兴趣小组测量一座大桥高度,如图所示,他们在A处测得大桥最高点D的仰角为45°,在前方240m的C处测得大桥最高点D的仰角为60°,求该兴趣小组测得的大桥高度DB.(
某校数学兴趣小组测量一座大桥高度,如图所示,他们在A处测得大桥最高点D的仰角为45°,在前方240m的C处测得大桥最高点D的仰角为60°,求该兴趣小组测得的大桥高度DB.(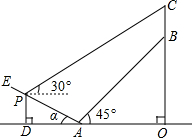 如图所示某人准备测量山顶铁塔BC的高度.在山的对面有一斜坡AE,斜坡的坡度为1:2(即tanα=
如图所示某人准备测量山顶铁塔BC的高度.在山的对面有一斜坡AE,斜坡的坡度为1:2(即tanα=