题目内容
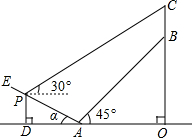 如图所示某人准备测量山顶铁塔BC的高度.在山的对面有一斜坡AE,斜坡的坡度为1:2(即tanα=
如图所示某人准备测量山顶铁塔BC的高度.在山的对面有一斜坡AE,斜坡的坡度为1:2(即tanα=| 1 |
| 2 |
| 3 |
考点:解直角三角形的应用-仰角俯角问题,解直角三角形的应用-坡度坡角问题
专题:
分析:过P点作PF⊥OC于点F,则∠PFC=90°.先由△AOB是等腰直角三角形,得出BO=AO=200米.由斜坡的坡度为1:2,PD=50米,得出AD=2PD=100米,则OD=AD+AO=300米.再由四边形PDOF为矩形,求出OF=PD=50米,PF=OD=300米,则BF=BO-OF=150米,然后解Rt△PFC,得出CF=PF•tan∠CPF=100
米,根据CB=CF-BF即可求出塔高BC.
| 3 |
解答: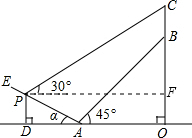 解:如图,过P点作PF⊥OC于点F,则∠PFC=90°.
解:如图,过P点作PF⊥OC于点F,则∠PFC=90°.
由题意得∠CPF=30°,∠BAO=45°,
∴∠OBA=∠BAO=45°,
∴BO=AO=200米.
∵斜坡的坡度为1:2,PD=50米,
∴AD=2PD=2×50=100(米),
∴OD=AD+AO=100+200=300(米).
∵四边形PDOF为矩形,
∴OF=PD=50米,PF=OD=300米,
∴BF=BO-OF=200-50=150(米).
在Rt△PFC中,tan∠CPF=
,
∴CF=PF•tan∠CPF=300×tan30°=300×
=100
(米),
∴CB=CF-BF=100
-150≈100×1.732-150=23.2≈23(米).
答:塔高BC约为23米.
 解:如图,过P点作PF⊥OC于点F,则∠PFC=90°.
解:如图,过P点作PF⊥OC于点F,则∠PFC=90°.由题意得∠CPF=30°,∠BAO=45°,
∴∠OBA=∠BAO=45°,
∴BO=AO=200米.
∵斜坡的坡度为1:2,PD=50米,
∴AD=2PD=2×50=100(米),
∴OD=AD+AO=100+200=300(米).
∵四边形PDOF为矩形,
∴OF=PD=50米,PF=OD=300米,
∴BF=BO-OF=200-50=150(米).
在Rt△PFC中,tan∠CPF=
| CF |
| PF |
∴CF=PF•tan∠CPF=300×tan30°=300×
| ||
| 3 |
| 3 |
∴CB=CF-BF=100
| 3 |
答:塔高BC约为23米.
点评:本题考查解直角三角形的应用-仰角俯角问题及坡度坡角问题,难度适中.要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
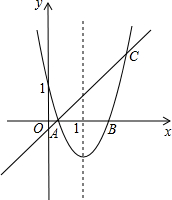 如图,一次函数y=x-
如图,一次函数y=x-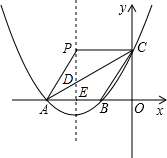 如图,已知抛物线y=ax2+4ax+t(a>0)交x轴于A、B两点,交y轴于点C,点B的坐标为(-1,0).
如图,已知抛物线y=ax2+4ax+t(a>0)交x轴于A、B两点,交y轴于点C,点B的坐标为(-1,0). 如图,已知矩形ABCD,
如图,已知矩形ABCD, 如图,直线a、b被直线c所截,且a∥b,如果∠1=66°,那么∠2=.
如图,直线a、b被直线c所截,且a∥b,如果∠1=66°,那么∠2=.