题目内容
先化简,再求代数式(1-
)+
的值,其中x是不等式组
的整数解.
| 2 |
| x+2 |
| x2-1 |
| x+3 |
|
考点:分式的化简求值,一元一次不等式组的整数解
专题:
分析:先根据分式混合运算的法则把原式进行化简,再代入合适的x的值代入进行计算即可.
解答:解:原式=[
-
]+
=
+
=
+
=
+
=
,
解
得,1<x<3,不等式组
的整数解为2,
当x=2时,原式=
=1.6.
| x+2 |
| x+2 |
| 2 |
| x+2 |
| x2-1 |
| x+3 |
=
| x |
| x+2 |
| x2-1 |
| x+3 |
=
| x2+3x |
| (x+2)(x+3) |
| (x+2)(x2-1) |
| (x+2)(x+3) |
=
| x2+3x |
| (x+2)(x+3) |
| x2+3x+x3-x+2x2-2 |
| (x+2)(x+3) |
=
| x3+4x2+5x-2 |
| (x+2)(x+3) |
解
|
|
当x=2时,原式=
| 8+16+10-2 |
| 20 |
点评:本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
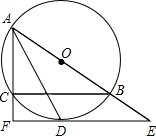 如图,AB是⊙O的直径,C为⊙O上一点,∠BAC的平分线交⊙O于点D,过点D作EF∥BC,交AB、AC的延长线于点E、F.
如图,AB是⊙O的直径,C为⊙O上一点,∠BAC的平分线交⊙O于点D,过点D作EF∥BC,交AB、AC的延长线于点E、F.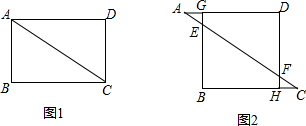
 如图,已知矩形ABCD,
如图,已知矩形ABCD, 在已建立直角坐标系的4×4正方形方格纸中,若每个小正方形的边长为1,在4×4方格纸中平移一次线段BC后的像为AD,以A,B,C,D为顶点的四边形是菱形,
在已建立直角坐标系的4×4正方形方格纸中,若每个小正方形的边长为1,在4×4方格纸中平移一次线段BC后的像为AD,以A,B,C,D为顶点的四边形是菱形,