Question

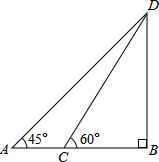某校数学兴趣小组测量一座大桥高度，如图所示，他们在A处测得大桥最高点D的仰角为45°，在前方240m的C处测得大桥最高点D的仰角为60°，求该兴趣小组测得的大桥高度DB．（

3

≈1，73，结果保留到10位）

Answer 1

考点：解直角三角形的应用-仰角俯角问题

专题：

分析：分别在Rt△ABD和Rt△BCD中，用BD表示出AB、BC的长，进而由AC=AB-BC=240求出DB的长．

解答：解：根据题意，可知∠A=45°，∠DCB=60°，AC=240m．设DB=x．
在Rt△ABD中，
∵∠A=∠BDA=45°，
∴BD=AB=x．
在Rt△BCD中，tan∠DCB=

DB

BC

，
∴BC=

DB

tan60°

=

3

3

DB=

3

3

x．
又∵AB-BC=AC，
∴x-

3

3

x=240，
∴x=120（3+

3

）≈5.7×10²m．
答：该兴趣小组测得的大桥高度DB约为5.7×10²m．

点评：本题考查仰角的知识．要求学生能借助仰角构造直角三角形并解直角三角形，注意数形结合思想与方程思想的应用．