题目内容
(1)计算:-2-2+(-
)-3-(9-π)0+|-4|
(2)计算:(-
)2•(2xy)2-x(x3y2-2x2y)
(3)化简求值:[(x+2y)2-(x+y)(3x-y)-5y2]÷(2x),其中x=-2,y=
.
| 1 |
| 2 |
(2)计算:(-
| 1 |
| 3 |
(3)化简求值:[(x+2y)2-(x+y)(3x-y)-5y2]÷(2x),其中x=-2,y=
| 1 |
| 2 |
考点:整式的混合运算—化简求值,整式的混合运算,零指数幂,负整数指数幂
专题:
分析:(1)先求出每一部分的值,再合并即可;
(2)先算乘方,再算乘法,最后合并即可;
(3)先算乘法,再合并同类项,最后算除法,代入求出即可.
(2)先算乘方,再算乘法,最后合并即可;
(3)先算乘法,再合并同类项,最后算除法,代入求出即可.
解答:解:(1)原式=-
-8-1+4
=-5
;
(2)原式=
•4x2y2-x4y2+2x3y
=
x2y2-x4y2+2x3y;
(3)原式=[x2+4xy+4y2-3x2+xy-3xy+y2-5y2]÷(2x)
=(-2x2+2xy)÷(2x)
=-x+y,
当x=-2,y=
时,原式=-(-2)+
=2
.
| 1 |
| 4 |
=-5
| 1 |
| 4 |
(2)原式=
| 1 |
| 9 |
=
| 4 |
| 9 |
(3)原式=[x2+4xy+4y2-3x2+xy-3xy+y2-5y2]÷(2x)
=(-2x2+2xy)÷(2x)
=-x+y,
当x=-2,y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了零指数幂,负整数指数幂,整式的混合运算和求值的应用,主要考查学生的计算能力和化简能力,题目比较好,难度适中.

练习册系列答案
相关题目
不等式组
的解集是( )
|
| A、x>2 | B、x>1 |
| C、1<x<2 | D、无解 |
 如图,三个等边三角形如图放置,若∠1=70°,则∠2+∠3=( )
如图,三个等边三角形如图放置,若∠1=70°,则∠2+∠3=( )| A、110° | B、105° |
| C、100° | D、95° |
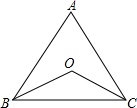 如图所示,在△ABC中,AB=AC,∠ABC和∠ACB的平分线相交于点O.试判断△OBC的形状,并说明理由.
如图所示,在△ABC中,AB=AC,∠ABC和∠ACB的平分线相交于点O.试判断△OBC的形状,并说明理由.
 如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,记四边形A1ABB1的面积为S1;再分别取A1C、B1C的中点A2、B2,记四边形A2A1B1B2的面积为S2;再分别取A2C、B2C的中点A3、B3,依次取下去…
如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,记四边形A1ABB1的面积为S1;再分别取A1C、B1C的中点A2、B2,记四边形A2A1B1B2的面积为S2;再分别取A2C、B2C的中点A3、B3,依次取下去…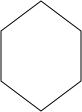 如图,表示一个正六菱柱形状的高大建筑物的俯视图.若该建筑物的高度为150米,底面正六边形的边长为50米.
如图,表示一个正六菱柱形状的高大建筑物的俯视图.若该建筑物的高度为150米,底面正六边形的边长为50米.