题目内容
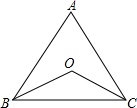 如图所示,在△ABC中,AB=AC,∠ABC和∠ACB的平分线相交于点O.试判断△OBC的形状,并说明理由.
如图所示,在△ABC中,AB=AC,∠ABC和∠ACB的平分线相交于点O.试判断△OBC的形状,并说明理由.考点:等腰三角形的判定与性质
专题:
分析:根据等腰三角形的性质得出∠ABC=∠ACB,根据角平分线定义得出∠OBC=
∠ABC,∠OCB=
∠ACB,求出∠OBC=∠OCB,推出OB=OC即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:△OBC的形状是等腰三角形,
理由是:∵AB=AC,
∴∠ABC=∠ACB,
∵∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=
∠ABC,∠OCB=
∠ACB,
∴∠OBC=∠OCB,
∴OB=OC,
即△OBC是等腰三角形.
理由是:∵AB=AC,
∴∠ABC=∠ACB,
∵∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠OBC=∠OCB,
∴OB=OC,
即△OBC是等腰三角形.
点评:本题考查了等腰三角形的性质和判定的应用,注意:等角对等边.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
不等式2-m<x+m的解集为x>2,则m的值为( )
| A、4 | ||
| B、2 | ||
| C、0 | ||
D、
|
下列性质中,正方形具有而矩形不一定具有的性质是( )
| A、对角线互相垂直 |
| B、对角线互相平分 |
| C、对角线相等 |
| D、四个角都是直角 |
 如图,直线a∥b,若∠1=120°,则∠2等于( )
如图,直线a∥b,若∠1=120°,则∠2等于( )| A、60° | B、80° |
| C、120° | D、150° |
 如图,在四边形ABCD中,AB∥CD,E为BC上一点,且∠BAE=50°,∠CDE=40°,若AE=4,DE=5,则AD=
如图,在四边形ABCD中,AB∥CD,E为BC上一点,且∠BAE=50°,∠CDE=40°,若AE=4,DE=5,则AD=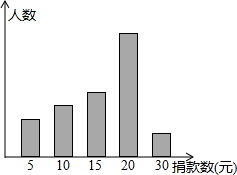 某中学对“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,如图是根据这组数据绘制的统计图,图中从左到右各长方形高度之比为3:4:5:8:2,又知此次调查中捐15元和20元得人数共39人.
某中学对“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,如图是根据这组数据绘制的统计图,图中从左到右各长方形高度之比为3:4:5:8:2,又知此次调查中捐15元和20元得人数共39人.