题目内容
如图,∠1=∠2,∠3=∠4,求证:AB=AC.


考点:全等三角形的判定与性质
专题:证明题
分析:根据等角的补角相等求出∠ADC=∠ADB,根据ASA推出△ADC≌△ADB,根据全等三角形的性质得出即可.
解答:证明:∵∠3=∠4,
∴180°-∠4=180°-∠3,
即:∠ADC=∠ADB,
在△ADC和△ADB中:
∴△ADC≌△ADB,
∴AB=AC.
∴180°-∠4=180°-∠3,
即:∠ADC=∠ADB,
在△ADC和△ADB中:
|
∴△ADC≌△ADB,
∴AB=AC.
点评:本题考查了全等三角形的性质和判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应边相等,对应角相等.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目

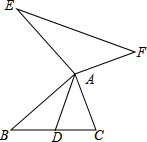 已知,如图:AD是△ABC的中线,AE⊥AB,AE=AB,AF⊥AC,AF=AC,连结EF.试猜想线段AD与EF的关系,并证明.
已知,如图:AD是△ABC的中线,AE⊥AB,AE=AB,AF⊥AC,AF=AC,连结EF.试猜想线段AD与EF的关系,并证明. 在如图所示的方格中有两个格点A,B,请再选择一个格点(用C表示),连接A,B,C,使△ABC成为一个等腰三角形,这样的等腰三角形一共可以连出
在如图所示的方格中有两个格点A,B,请再选择一个格点(用C表示),连接A,B,C,使△ABC成为一个等腰三角形,这样的等腰三角形一共可以连出