题目内容
 已知,如图,在△ABC中,点D是BC的中点,点E是BD的中点,AB=BD
已知,如图,在△ABC中,点D是BC的中点,点E是BD的中点,AB=BD求证:∠CAD=∠EAD.
考点:含30度角的直角三角形,等边三角形的判定与性质
专题:证明题
分析:过点A作AF平行且等于BD,判断出四边形ABCF为菱形,根据菱形的四条边都相等可得AF=DF=BD,菱形的对角线平分一组对角线可得∠ADB=∠ADF,连接FC,得到四边形ADCF为平行四边形,根据平行四边形对角线互相平分可得DF=DG,从而得到DE=DG,再利用“边角边”证明△AED和△AGD全等,根据全等三角形对应角相等证明即可.
解答: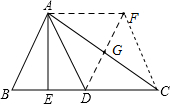 证明:如图,过点A作AF平行且等于BD,
证明:如图,过点A作AF平行且等于BD,
所以,四边形ABDF是平行四边形,
∵AB=BD,
∴ABCF为菱形,
∴AF=DF=BD,∠ADB=∠ADF,
连接FC,
又∵BD=CD,
∴四边形ADCF为平行四边形,
∴G为DF中点,
∵点E是BD的中点,
∴DE=
BD,
∴DE=DG,
在△AED和△AGD中,
,
∴△AED≌△AGD(SAS),
∴∠CAD=∠EAD.
 证明:如图,过点A作AF平行且等于BD,
证明:如图,过点A作AF平行且等于BD,所以,四边形ABDF是平行四边形,
∵AB=BD,
∴ABCF为菱形,
∴AF=DF=BD,∠ADB=∠ADF,
连接FC,
又∵BD=CD,
∴四边形ADCF为平行四边形,
∴G为DF中点,
∵点E是BD的中点,
∴DE=
| 1 |
| 2 |
∴DE=DG,
在△AED和△AGD中,
|
∴△AED≌△AGD(SAS),
∴∠CAD=∠EAD.
点评:本题考查了菱形的判定与性质,平行四边形的判定与性质,全等三角形的判定与性质,综合题,难度较大,作辅助线构造出菱形和全等三角形是解题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
如果一个三角形的三边长a,b,c满足a2+b2+c2+388=10a+24b+26c,那么这个三角形一定是( )
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、等腰三角形 |
若x2-4x+p=(x+q)2,则p、q的值分别是( )
| A、4、2 | B、4、-2 |
| C、-4、-2 | D、-4、2 |
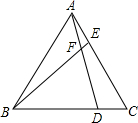 如图,已知△ABC为等边三角形,点D、E分别在边BC、AC上,且AE=CD,AD与BE交于点F.
如图,已知△ABC为等边三角形,点D、E分别在边BC、AC上,且AE=CD,AD与BE交于点F.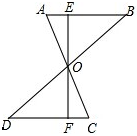 如图,AC与BD互相平分且相交于点O,点E、F分别在AB、CD上,且AE=CF,试利用“中心对称”的有关知识,说明点E、O、F在同一直线上且OE=OF.
如图,AC与BD互相平分且相交于点O,点E、F分别在AB、CD上,且AE=CF,试利用“中心对称”的有关知识,说明点E、O、F在同一直线上且OE=OF.