题目内容
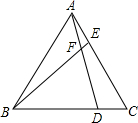 如图,已知△ABC为等边三角形,点D、E分别在边BC、AC上,且AE=CD,AD与BE交于点F.
如图,已知△ABC为等边三角形,点D、E分别在边BC、AC上,且AE=CD,AD与BE交于点F.(1)证明:△ABE≌△CAD;
(2)求∠BFD的度数.
考点:全等三角形的判定与性质
专题:
分析:(1)根据等边三角形的性质就可以得出∠BAC=∠C=60°,AB=AC,由SAS就可以得出△ABE≌△CAD,
(2)由△ABE≌△CAD就可以得出∠ABE=∠CAD,由外角与内角的关系就可以得出∠BFD=∠ABE+∠BAD,得出∠BFD=∠BAD+∠CAD=60°.
(2)由△ABE≌△CAD就可以得出∠ABE=∠CAD,由外角与内角的关系就可以得出∠BFD=∠ABE+∠BAD,得出∠BFD=∠BAD+∠CAD=60°.
解答:解:(1)∵△ABC为等边三角形,
∴∠BAC=∠C=60°,AB=AC.
在△ABE和△CAD中,
,
∴△ABE≌△CAD(SAS);
(2)∵△ABE≌△CAD,
∴∠ABE=∠CAD.
∵∠BFD=∠ABE+∠BAD,
∴∠BFD=∠BAD+∠CAD=∠BAC=60°.
答:∠BFD的度数为60°.
∴∠BAC=∠C=60°,AB=AC.
在△ABE和△CAD中,
|
∴△ABE≌△CAD(SAS);
(2)∵△ABE≌△CAD,
∴∠ABE=∠CAD.
∵∠BFD=∠ABE+∠BAD,
∴∠BFD=∠BAD+∠CAD=∠BAC=60°.
答:∠BFD的度数为60°.
点评:本题考查了等边三角形的性质的运用,全等三角形的判定及性质的运用,三角形的外角与内角的关系的运用,解答时证明三角形的全等是关键.

练习册系列答案
相关题目
已知△ABC≌△A1B1C1,且△ABC的周长是20,AB=8,BC=5,那么A1B1等于( )
| A、5 | B、6 | C、7 | D、8 |
一架飞机在两城市之间飞行,顺风需要3小时,逆风需要3小时20分,已知风速是20千米/小时,则两城市的距离为( )
| A、1000千米 |
| B、1100千米 |
| C、1200千米 |
| D、1300千米 |
 已知,如图,在△ABC中,点D是BC的中点,点E是BD的中点,AB=BD
已知,如图,在△ABC中,点D是BC的中点,点E是BD的中点,AB=BD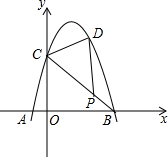 如图,抛物线y=-x2+bx+c经过点A、B、C,已知A(-1,0),C(0,3).P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,点P的坐标为
如图,抛物线y=-x2+bx+c经过点A、B、C,已知A(-1,0),C(0,3).P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,点P的坐标为