题目内容
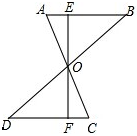 如图,AC与BD互相平分且相交于点O,点E、F分别在AB、CD上,且AE=CF,试利用“中心对称”的有关知识,说明点E、O、F在同一直线上且OE=OF.
如图,AC与BD互相平分且相交于点O,点E、F分别在AB、CD上,且AE=CF,试利用“中心对称”的有关知识,说明点E、O、F在同一直线上且OE=OF.考点:中心对称
专题:
分析:连接AD、BC,根据对角线互相平分的四边形是平行四边形求出四边形ABCD是平行四边形,再根据平行四边形的中心对称性判断出E、F是对称点,然后根据轴对称性解答.
解答: 证明:如图,连接AD、BC,
证明:如图,连接AD、BC,
∵AC与BD互相平分且相交于点O,
∴四边形ABCD是平行四边形,
∴点O是平行四边形ABCD的对称中心,
∵AE=CF,
∴点E、F是对称点,
∴点E、O、F在同一直线上且OE=OF.
 证明:如图,连接AD、BC,
证明:如图,连接AD、BC,∵AC与BD互相平分且相交于点O,
∴四边形ABCD是平行四边形,
∴点O是平行四边形ABCD的对称中心,
∵AE=CF,
∴点E、F是对称点,
∴点E、O、F在同一直线上且OE=OF.
点评:本题考查了中心对称,主要利用了平行四边形的判定与中心对称性,对称点的连线比过对称中心并且被对称中心平分,熟记性质并作辅助线构造出平行四边形是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
一架飞机在两城市之间飞行,顺风需要3小时,逆风需要3小时20分,已知风速是20千米/小时,则两城市的距离为( )
| A、1000千米 |
| B、1100千米 |
| C、1200千米 |
| D、1300千米 |
 已知,如图,在△ABC中,点D是BC的中点,点E是BD的中点,AB=BD
已知,如图,在△ABC中,点D是BC的中点,点E是BD的中点,AB=BD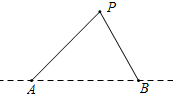 国外船只,除特许外,不得进入我国海洋100海里以内区域.如图,设A,B是我们观察站A和B之间为150海里,海岸线是过A,B的一条直线,一外国船只在P点,在A点测到∠BAP=45°,同时在B点测得∠ABP=60°,问此时是否要向外国船只发出警告?
国外船只,除特许外,不得进入我国海洋100海里以内区域.如图,设A,B是我们观察站A和B之间为150海里,海岸线是过A,B的一条直线,一外国船只在P点,在A点测到∠BAP=45°,同时在B点测得∠ABP=60°,问此时是否要向外国船只发出警告?