题目内容
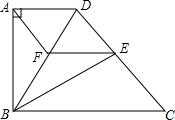 如图,在直角梯形ABCD中,AD∥BC,AB⊥AD,若沿对角线BD翻折梯形ABCD,点A将恰好落在腰CD上的点E处.
如图,在直角梯形ABCD中,AD∥BC,AB⊥AD,若沿对角线BD翻折梯形ABCD,点A将恰好落在腰CD上的点E处.(1)求证:BC=CD;
(2)若点F在BD上,AF∥CD,连接EF,判断四边形ADEF是什么特殊四边形,证明你的结论.
考点:直角梯形,翻折变换(折叠问题)
专题:
分析:(1)由直角梯形ABCD沿对角线BD翻折,点A将恰好落在腰CD上的点E处.可得∠ADB=∠BDC,由AD∥BC,可得∠ADB=∠DBC,进而得出∠ADB=∠DBC,即可得BC=CD;
(2)由直角梯形ABCD沿对角线BD翻折梯形ABCD,点A将恰好落在腰CD上的点E处.可得BA=BE,∠ABF=∠EBF,BF=BF,即可得出△ABF≌△EBF,可得AF=EF,∠AFB=∠EFB,进而得出∠AFD=∠EFD,可得∠EFD=∠EDF,得出EF=ED,由AD=ED,可得AD=ED=EF=AF,即可得出ADEF是菱形.
(2)由直角梯形ABCD沿对角线BD翻折梯形ABCD,点A将恰好落在腰CD上的点E处.可得BA=BE,∠ABF=∠EBF,BF=BF,即可得出△ABF≌△EBF,可得AF=EF,∠AFB=∠EFB,进而得出∠AFD=∠EFD,可得∠EFD=∠EDF,得出EF=ED,由AD=ED,可得AD=ED=EF=AF,即可得出ADEF是菱形.
解答:解:(1)∵直角梯形ABCD沿对角线BD翻折梯形ABCD,点A将恰好落在腰CD上的点E处.
∴∠ADB=∠BDC,
∵AD∥BC,
∴∠ADB=∠DBC,
∴∠ADB=∠DBC,
∴BC=CD;
(2)∵直角梯形ABCD沿对角线BD翻折梯形ABCD,点A将恰好落在腰CD上的点E处.
∴BA=BE,∠ABF=∠EBF,BF=BF,
在△ABF和△EBF中,
,
∴△ABF≌△EBF(SAS),
∴AF=EF,∠AFB=∠EFB,
∴∠AFD=∠EFD,
∴∠EFD=∠EDF,
∴EF=ED,
∵AD=ED,
∴AD=ED=EF=AF,
∴ADEF是菱形.
∴∠ADB=∠BDC,
∵AD∥BC,
∴∠ADB=∠DBC,
∴∠ADB=∠DBC,
∴BC=CD;
(2)∵直角梯形ABCD沿对角线BD翻折梯形ABCD,点A将恰好落在腰CD上的点E处.
∴BA=BE,∠ABF=∠EBF,BF=BF,
在△ABF和△EBF中,
|
∴△ABF≌△EBF(SAS),
∴AF=EF,∠AFB=∠EFB,
∴∠AFD=∠EFD,
∴∠EFD=∠EDF,
∴EF=ED,
∵AD=ED,
∴AD=ED=EF=AF,
∴ADEF是菱形.
点评:本题主要考查了直角梯形及折叠问题,解题的关键是图形折叠前后边及角的大小不变.

练习册系列答案
相关题目
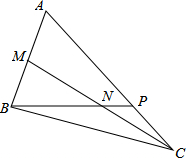 已知:M是AB的中点,AP=2PC,BP=4,求PN的长.
已知:M是AB的中点,AP=2PC,BP=4,求PN的长. 如图,同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,它们的斜边长为2.若△ABC固定不动,△AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合).设BE=m,CD=n.求m与n的函数关系式.
如图,同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,它们的斜边长为2.若△ABC固定不动,△AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合).设BE=m,CD=n.求m与n的函数关系式. 如图,已知∠1+∠2=180°,∠C=∠D,则∠A=∠F吗?为什么?
如图,已知∠1+∠2=180°,∠C=∠D,则∠A=∠F吗?为什么?