题目内容
1.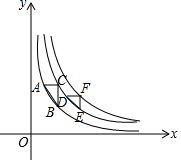 如图,△ABC和△DEF的各顶点分别在双曲线y=$\frac{1}{x}$,y=$\frac{2}{x}$,y=$\frac{3}{x}$在第一象限的图象上,若∠C=∠F=90°,AC∥DF∥x轴,BC∥EF∥y轴,则S△ABC-S△DEF=( )
如图,△ABC和△DEF的各顶点分别在双曲线y=$\frac{1}{x}$,y=$\frac{2}{x}$,y=$\frac{3}{x}$在第一象限的图象上,若∠C=∠F=90°,AC∥DF∥x轴,BC∥EF∥y轴,则S△ABC-S△DEF=( )| A. | $\frac{1}{12}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{5}{12}$ |
分析 设点C(a,$\frac{2}{a}$),点F(b,$\frac{3}{b}$),由AC∥DF∥x轴、BC∥EF∥y轴利用反比例函数图象上点的坐标特征即可求出点A、B、D、E的坐标,从而得出AC、BC、DF、EF的长度,再利用三角形的面积公式即可求出S△ABC-S△DEF的值.
解答 解:设点C(a,$\frac{2}{a}$),点F(b,$\frac{3}{b}$),则点A($\frac{a}{2}$,$\frac{2}{a}$)、B(a,$\frac{1}{a}$)、D($\frac{2b}{3}$,$\frac{3}{b}$)、E(b,$\frac{2}{b}$),
∴AC=$\frac{a}{2}$,BC=$\frac{1}{a}$,DF=$\frac{b}{3}$,EF=$\frac{1}{b}$,
∴S△ABC-S△DEF=$\frac{1}{2}$AC•BC-$\frac{1}{2}$DF•EF=$\frac{1}{4}$-$\frac{1}{6}$=$\frac{1}{12}$.
故选A.
点评 本题考查了反比例函数图象上点的坐标特征以及三角形的面积,根据点C、F的坐标表示出点A、B、D、E的坐标是解题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
11.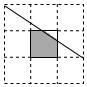 如图,有16个格点,每个格点小正方形的面积为1,给图中间的小正方形内任意投点P,则点P落在图中阴影部分的概率为( )
如图,有16个格点,每个格点小正方形的面积为1,给图中间的小正方形内任意投点P,则点P落在图中阴影部分的概率为( )
 如图,有16个格点,每个格点小正方形的面积为1,给图中间的小正方形内任意投点P,则点P落在图中阴影部分的概率为( )
如图,有16个格点,每个格点小正方形的面积为1,给图中间的小正方形内任意投点P,则点P落在图中阴影部分的概率为( )| A. | $\frac{5}{6}$ | B. | $\frac{7}{8}$ | C. | $\frac{9}{10}$ | D. | $\frac{11}{12}$ |
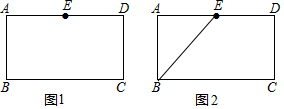
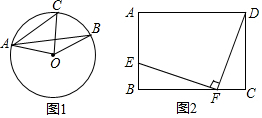
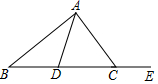 已知:如图,AD是△ABC的中线,∠ACE是△ABC的外角.
已知:如图,AD是△ABC的中线,∠ACE是△ABC的外角.