题目内容
20.若-4≤a≤0,则代数式$\sqrt{9+6a+{a}^{2}}$+$\sqrt{{a}^{2}-10a+25}$的最大值为10.分析 根据二次根式的性质进行化简,再根据a的取值范围进行分类讨论,即可解答.
解答 解:$\sqrt{9+6a+{a}^{2}}$+$\sqrt{{a}^{2}-10a+25}$
=$\sqrt{(3+a)^{2}}+\sqrt{(a-5)^{2}}$
=|3+a|+|a-5|
当-3≤a≤0,
∴3+a≥0,a-5<0,
原式=3+a-a+5=8,
当-4≤a<-3时,3+a<0,a-5<0,
原式=-3-a-a+5=-2a+2,
此时当a=-4时,原式有最大值,-2×(-4)+2=10,
∴代数式$\sqrt{9+6a+{a}^{2}}$+$\sqrt{{a}^{2}-10a+25}$的最大值为10.
故答案为:10.
点评 本题考查了二次根式的性质,解决本题的关键是根据二次根式的性质进行化简.

练习册系列答案
相关题目
11.多项式x2-mxy+9y2能用完全平方因式分解,则m的值是( )
| A. | 3 | B. | 6 | C. | ±3 | D. | ±6 |
12. 如图,菱形ABCD的周长为16,∠ABC=120°,则AC的长为( )
如图,菱形ABCD的周长为16,∠ABC=120°,则AC的长为( )
 如图,菱形ABCD的周长为16,∠ABC=120°,则AC的长为( )
如图,菱形ABCD的周长为16,∠ABC=120°,则AC的长为( )| A. | 4$\sqrt{3}$ | B. | 4 | C. | 2$\sqrt{3}$ | D. | 2 |
9.如果直线y=3x+6与y=2x-4交点坐标为(a,b),则解为$\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$的方程组是( )
| A. | $\left\{\begin{array}{l}{y-3x=6}\\{2y+x=-4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{y-3x=6}\\{2y-x=4}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{3x-y=6}\\{3x-y=4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{3x-y=-6}\\{2x-y=4}\end{array}\right.$ |
10.若关于x的方程x2+px+q=0(p、q为常数)的两个实数根分别为2和-3,则p、q的值分别为( )
| A. | 2,-3 | B. | -1,-6 | C. | 1,-6 | D. | 1,6 |
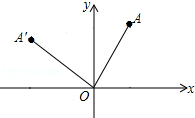 如图,在平面直角坐标系中,已知点A(6,8),将OA绕坐标原点O逆时针旋转90°至OA′,则点A′的坐标是(-8,6).
如图,在平面直角坐标系中,已知点A(6,8),将OA绕坐标原点O逆时针旋转90°至OA′,则点A′的坐标是(-8,6).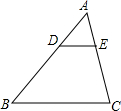 如图,△ABC中,DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,DE=3,则BC边的长是( )
如图,△ABC中,DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,DE=3,则BC边的长是( )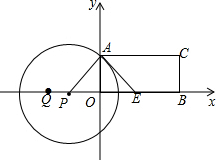 如图,矩形ABCD,A(0,3)、B(6,0),点E在OB上,∠AEO=45°,点P从点Q(-4,0)出发,沿x轴向右以每秒1个单位长的速度运动,运动时间为t秒.
如图,矩形ABCD,A(0,3)、B(6,0),点E在OB上,∠AEO=45°,点P从点Q(-4,0)出发,沿x轴向右以每秒1个单位长的速度运动,运动时间为t秒. 已知:如图,△CBE是一个锐角三角形,分别以CB,CE为边向外侧作等边三角形ABC和等边三角形CDE,连接AE、BD.
已知:如图,△CBE是一个锐角三角形,分别以CB,CE为边向外侧作等边三角形ABC和等边三角形CDE,连接AE、BD.