题目内容
13.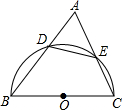 如图,在锐角△ABC中,以BC为直径的半圆O分别交AB,AC于D,E两点,且cosA=$\frac{\sqrt{3}}{3}$,则S△ADE:S四边形DBCE的值为$\frac{1}{2}$.
如图,在锐角△ABC中,以BC为直径的半圆O分别交AB,AC于D,E两点,且cosA=$\frac{\sqrt{3}}{3}$,则S△ADE:S四边形DBCE的值为$\frac{1}{2}$.
分析 连接BE,由∠A得余弦值可得到AE、AB的比例关系;易证得△ADE∽△ACB,那么AE、AB的比即为两个三角形的相似比,进而可求出两个三角形的面积比,也就能求出△ADE、四边形BDEC的面积比.
解答 解:连接BE;
∵BC是⊙O的直径
∴∠BEC=90°;
在Rt△ABE中,cosA=$\frac{\sqrt{3}}{3}$,即$\frac{AE}{AB}=\frac{\sqrt{3}}{3}$;
∵四边形BEDC内接于⊙O,
∴∠ADE=∠ACB,∠AED=∠ABC,
∴△ADE∽△ABC,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}=(\frac{AE}{AB})^{2}$=$\frac{1}{3}$;
所以S△ADE:S四边形DBCE的值为$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 此题主要考查了圆内接四边形的性质以及相似三角形的判定和性质,能够将∠A的余弦值转换为△ADE、△ACB的相似比,是解决此题的关键.

练习册系列答案
相关题目
5.-1的倒数是( )
| A. | -1 | B. | 0 | C. | 1 | D. | ±1 |
2.关于x的方程x+2=ax的解为( )
| A. | 正数 | B. | 负数 | C. | 0 | D. | 以上答案都不对 |
3.把方程8x-1=5x+2移项可得( )
| A. | 8x+5x=2-1 | B. | 8x-5x=-2-1 | C. | 8x-5x=2+1 | D. | 8x+5x=2+1 |
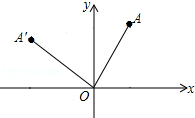 如图,在平面直角坐标系中,已知点A(6,8),将OA绕坐标原点O逆时针旋转90°至OA′,则点A′的坐标是(-8,6).
如图,在平面直角坐标系中,已知点A(6,8),将OA绕坐标原点O逆时针旋转90°至OA′,则点A′的坐标是(-8,6).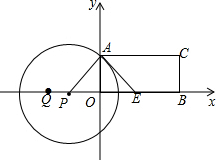 如图,矩形ABCD,A(0,3)、B(6,0),点E在OB上,∠AEO=45°,点P从点Q(-4,0)出发,沿x轴向右以每秒1个单位长的速度运动,运动时间为t秒.
如图,矩形ABCD,A(0,3)、B(6,0),点E在OB上,∠AEO=45°,点P从点Q(-4,0)出发,沿x轴向右以每秒1个单位长的速度运动,运动时间为t秒.